
【题目】如图,将一副直角三角形的直角顶点C叠放一起
(1)如图1,若CE恰好是∠ACD的角平分线,请你猜想此时CD是不是的∠ECB的角平分线?并简述理由;
(2)如图1,若∠ECD=α,CD在∠ECB的内部,请猜想∠ACE与∠DCB是否相等?并简述理由;
(3)在如图2的条件下,请问∠ECD与∠ACB的和是多少?并简述理由.
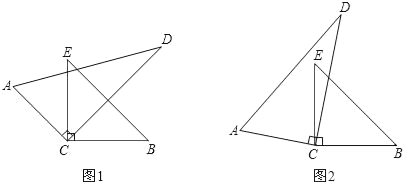
【答案】(1)CD是∠ECB的角平分线,见解析;(2)∠ACE=∠DCB,见解析;(3)∠DCE+∠ACB=180°,见解析.
【解析】
(1)CD是∠ECB的角平分线,求出∠ECD=∠BCD=45°即可证明;(2)∠ACE=∠DCB,求出∠ACE=∠DCB=90°﹣α即可;(3)∠DCE+∠ACB=180°,根据∠DCE+∠ACB=∠DCE+∠ACE+∠BCE=∠ACD+∠BCE即可进行求解证明.
解:(1)CD是∠ECB的角平分线,
理由是:∵∠ACD=90°,CE是∠ACD的角平分线,
∴∠ECD=![]() ∠ACD=45°,
∠ACD=45°,
∴∠BCD=90°﹣∠ECD=45°=∠ECD,
即CD是∠ECB的角平分线;
(2)∠ACE=∠DCB,
理由是:∵∠ACD=∠BCE=90°,∠ECD=α,
∴∠ACE=90°﹣α,∠DCB=90°﹣α,
∴∠ACE=∠DCB;
(3)∠DCE+∠ACB=180°,
理由是:∵∠ACD=∠BCE=90°,
∴∠DCE+∠ACB=∠DCE+∠ACE+∠BCE=∠ACD+∠BCE=90°+90°=180°,
即∠DCE+∠ACB=180°.


科目:初中数学 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
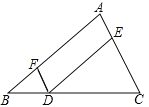
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
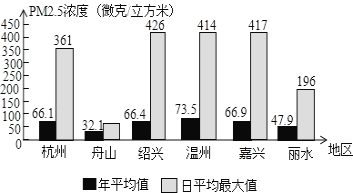
【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
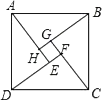
A. 8 B. 6 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
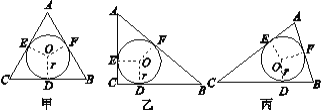
【题目】为了探索三角形的内切圆半径r与三角形的周长C、面积S之间的关系,在数学实验活动中,选取等边三角形图甲和直角三角形图乙进行研究.已知⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)用刻度尺分别量出表中未量度的△ABC的长,填入空格处,并计算出周长C和面积S(结果精确到0.1);
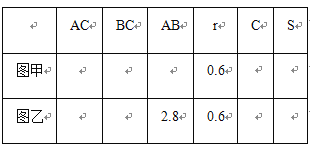
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与C,S之间的关系,判断这种关系对任意三角形(图丙)是否也成立,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】让我们轻松一下,做一个数字游戏。第一步:取一个自然数n1=5,计算n12+1得a1;第二步:算出a1的各位数字之和得n2,计算n22+1得a2;第三步,算出a2的各位数字之和得n3,计算n32+1得a3;…………以此类推,则a2019=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
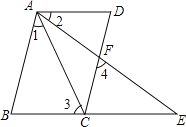
【题目】如图,已知AB∥CD,∠1=∠2,∠3=∠4,则AD∥BE.完成下列推理过程:
证明:∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠CAE+∠1=∠CAE+∠2
即∠ =∠
∴∠3=
∴AD∥BE( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com