
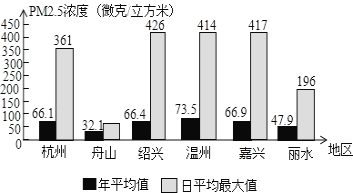
【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
科目:初中数学 来源: 题型:
【题目】某市地铁二号线某工段需要开挖土石方,计划每小时挖掘土石方700m3,现决定向一大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表:
租金(单位:元/台·时) | 土石方量(单位:m3/台·时) | |
甲型挖掘机 | 90 | 50 |
乙型挖掘机 | 100 | 60 |
⑴ 若租用甲、乙两种型号的挖掘机共13台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
⑵ 如果每小时支付的租金不超过1200元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)如图,已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
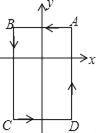
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).动点P从点A处出发,并按A﹣B﹣C﹣D﹣A﹣B…的规律在四边形ABCD的边上以每秒1个单位长的速度运动,运动时间为t秒.若t=2018秒,则点P所在位置的点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型建立)
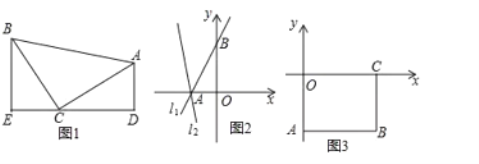
(1)如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(模型应用)
(2)已知直线![]() :
:![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至直线
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;
(3)如图3,长方形![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 、
、![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限.若
上的动点且在第四象限.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
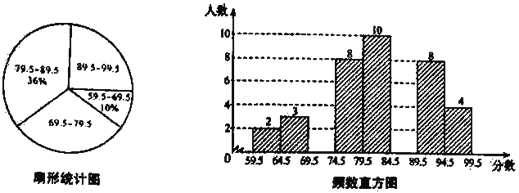
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
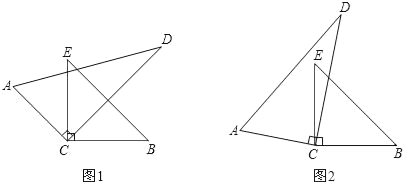
【题目】如图,将一副直角三角形的直角顶点C叠放一起
(1)如图1,若CE恰好是∠ACD的角平分线,请你猜想此时CD是不是的∠ECB的角平分线?并简述理由;
(2)如图1,若∠ECD=α,CD在∠ECB的内部,请猜想∠ACE与∠DCB是否相等?并简述理由;
(3)在如图2的条件下,请问∠ECD与∠ACB的和是多少?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年6月19日,重庆轨道十八号线(原5A线)项目加快建设动员大会在项目土建七标段施工现场矩形,预计改线2020年全面建成,届时有效环节主城南部交通拥堵,全线已完成桩点复测,滩子口站到黄桷坪站区间施工通道等9处工点打围,在此过程中,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了施工通道工点打围。下面能反映该工程施工道路y(米)与时间x(天)的关系的大致图像是( )
A.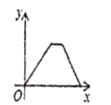 B.
B.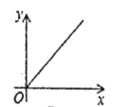 C.
C.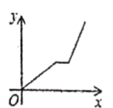 D.
D.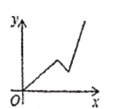
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°.
(1)若∠A=30°,b=![]() ,求∠B和a,c;
,求∠B和a,c;
(2)若a=4,b=5,求c(精确到0.1)和∠A,∠B(精确到1°).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com