
【题目】(模型建立)
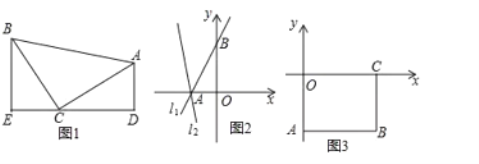
(1)如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(模型应用)
(2)已知直线![]() :
:![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至直线
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;
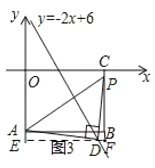
(3)如图3,长方形![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 、
、![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限.若
上的动点且在第四象限.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)见解析;(2)y=7x21;(3)D(4,2)或(![]() ,
,![]() ).
).
【解析】
(1)根据△ABC为等腰直角三角形,AD⊥ED,BE⊥ED,可判定![]() ;
;
(2)①过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,根据△CBD≌△BAO,得出BD=AO=3,CD=OB=4,求得C(4,7),最后运用待定系数法求直线l2的函数表达式;
(3)根据△APD是以点D为直角顶点的等腰直角三角形,当点D是直线y=2x+6上的动点且在第四象限时,分两种情况:当点D在矩形AOCB的内部时,当点D在矩形AOCB的外部时,设D(x,2x+6),分别根据△ADE≌△DPF,得出AE=DF,据此列出方程进行求解即可.
解:(1)证明:∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,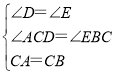 ,
,
∴![]() (AAS);
(AAS);
(2)①如图2,过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,
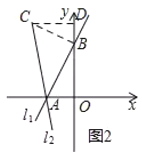
∵∠BAC=45°,
∴△ABC为等腰直角三角形,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=![]() x+4中,若y=0,则x=3;若x=0,则y=4,
x+4中,若y=0,则x=3;若x=0,则y=4,
∴A(3,0),B(0,4),
∴BD=AO=3,CD=OB=4,
∴OD=4+3=7,
∴C(4,7),
设l2的解析式为y=kx+b,则![]() ,
,
解得:![]() ,
,
∴l2的解析式为:y=7x21;
(3)D(4,2)或(![]() ,
,![]() ).
).
理由:当点D是直线y=2x+6上的动点且在第四象限时,分两种情况:
当点D在矩形AOCB的内部时,如图,过D作x轴的平行线EF,交直线OA于E,交BC于F,
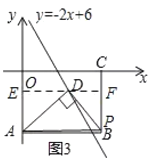
设D(x,2x+6),则OE=2x6,AE=6(2x6)=122x,DF=EFDE=8x,
由(1)可得,△ADE≌△DPF,则DF=AE,即:122x=8x,
解得x=4,
∴2x+6=2,
∴D(4,2),
此时,PF=ED=4,CP=6=CB,符合题意;
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
设D(x,2x+6),则OE=2x6,AE=OEOA=2x66=2x12,DF=EFDE=8x,
同理可得:△ADE≌△DPF,则AE=DF,即:2x12=8x,
解得x=![]() ,
,
∴2x+6=![]() ,
,
∴D(![]() ,
,![]() ),
),
此时,ED=PF=![]() ,AE=BF=
,AE=BF=![]() ,BP=PFBF=
,BP=PFBF=![]() <6,符合题意,
<6,符合题意,
综上所述,D点坐标为:(4,2)或(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
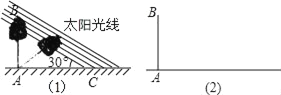
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
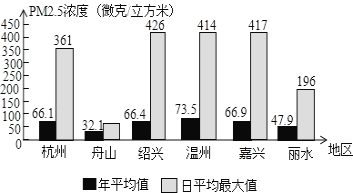
【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
查看答案和解析>>
科目:初中数学 来源: 题型:
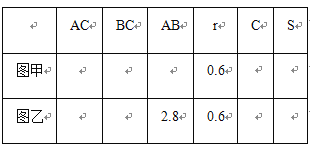
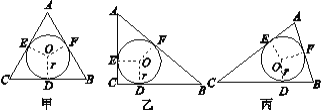
【题目】为了探索三角形的内切圆半径r与三角形的周长C、面积S之间的关系,在数学实验活动中,选取等边三角形图甲和直角三角形图乙进行研究.已知⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)用刻度尺分别量出表中未量度的△ABC的长,填入空格处,并计算出周长C和面积S(结果精确到0.1);
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与C,S之间的关系,判断这种关系对任意三角形(图丙)是否也成立,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
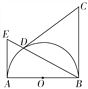
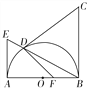
图4① 图4②
(1)如图①,若CD=CB,求证:CD为半圆O的切线;
(2)如图②,若点F在OB上,且FD⊥CD,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com