
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
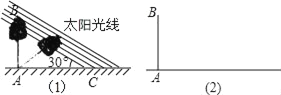
【答案】(1)树AB的高约为4![]() m;(2)8
m;(2)8![]() m.
m.
【解析】
(1)AB=ACtan30°=12×![]() =
=![]() (米).
(米).
答:树高约为![]() 米.
米.
(2)如图(2),B1N=AN=AB1sin45°=![]() ×
×![]() =
=![]() (米).
(米).
NC1=NB1tan60°=![]() ×
×![]() =
=![]() (米).
(米).
AC1=AN+NC1=![]() +
+![]() .
.
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2=![]() ;
;
(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,再根据当树与地面成60°角时影长最大,根据三角函数即可求解.


科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
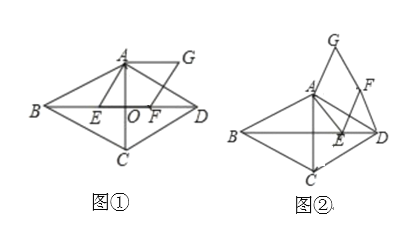
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司员工住在![]() 三个住宅区,已知
三个住宅区,已知![]() 区有2人,
区有2人,![]() 区有7人,
区有7人,![]() 区有12人,三个住宅区在同一条直线上,且
区有12人,三个住宅区在同一条直线上,且![]() ,
,![]() 是
是![]() 的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在
的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在![]() 四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
![]()
A.![]() 处B.
处B.![]() 处C.
处C.![]() 处D.
处D.![]() 处
处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并。立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇对,两船与黄岩岛的距离、
(3在渔政船驶往黄岩岛的过程中,求渔船从港口 出发经过多长时间与渔政船相距30海里?
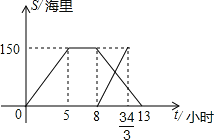
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则________后四边形ABQP为平行四边形.
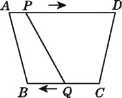
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁二号线某工段需要开挖土石方,计划每小时挖掘土石方700m3,现决定向一大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表:
租金(单位:元/台·时) | 土石方量(单位:m3/台·时) | |
甲型挖掘机 | 90 | 50 |
乙型挖掘机 | 100 | 60 |
⑴ 若租用甲、乙两种型号的挖掘机共13台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
⑵ 如果每小时支付的租金不超过1200元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 阅读理解
问题1:已知a、b、c、d为正数,![]() ,ac=bd,试说明a=d,b=c.
,ac=bd,试说明a=d,b=c.
我们通过构造几何模型解决代数问题. 注意到条件![]() ,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
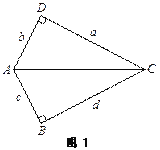
∵ac=bd,
∴AB·CD=BC·AD
∴![]()
请你按照以上思路继续完成说明.
⑵ 深入探究
问题2:若a>0,b>0,试比较![]() 和
和![]() 的大小.
的大小.
为此我们构造图2所示的几何模型,其中AB为直径, O为圆心,点C在半圆上,CD⊥AB 于D,AD=a,BD=b.
请你利用图2所示的几何模型解决提出的问题2.
⑶ 拓展运用
对于函数y=x+![]() ,求当x>0时,求y的取值范围.
,求当x>0时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在手工制作课上,老师组织七年级![]() 班的学生用硬纸制作圆柱形茶叶筒.七年级
班的学生用硬纸制作圆柱形茶叶筒.七年级![]() 班共有学生
班共有学生![]() 人,其中男生人数比女生人数少
人,其中男生人数比女生人数少![]() 人,并且每名学生每小时剪筒身
人,并且每名学生每小时剪筒身![]() 个或剪筒底
个或剪筒底![]() 个.
个.
(1)七年级![]() 班有男生、女生各多少人?
班有男生、女生各多少人?
(2)原计划男生负责剪筒底,女生负责剪筒身,要求一个筒身配两个筒底,那么每小时剪出的筒身与筒底能配套吗?如果不配套,那么如何进行人员调配,才能使每小时剪出的筒身与筒底刚好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
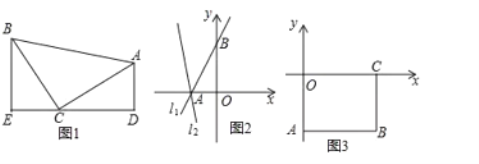
【题目】(模型建立)
(1)如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(模型应用)
(2)已知直线![]() :
:![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至直线
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;
(3)如图3,长方形![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 、
、![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限.若
上的动点且在第四象限.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com