
【题目】黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并。立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇对,两船与黄岩岛的距离、
(3在渔政船驶往黄岩岛的过程中,求渔船从港口 出发经过多长时间与渔政船相距30海里?
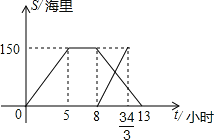
【答案】(1)当0≤t≤5时,s=30t;当5<t≤8时,s=150;当8<t≤13时,s=-30t+390(2)=60海里(3)9.6小时或10.5小时
【解析】解:(1)当0≤t≤5时,s=30t;当5<t≤8时,s=150;当8<t≤13时,s=-30t+390。
(2)设渔政船离港口的距离s与渔船离开港口的时间t之间的函数关系式为s=kt+b,则
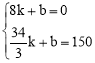 ,解得
,解得![]() 。∴s=45t-360。
。∴s=45t-360。
联立![]() ,解得
,解得![]() 。
。
∴渔船离黄岩岛的距离为150-90=60(海里)。
(3)∵![]() ,∴分两种情况:
,∴分两种情况:
①-30t+390-(45t-360)=30,解得t=9.6;
②45t-360-(-30t+390)=30,解得t=10.5。
∴当渔船离开港口9.6小时或10.5小时时,两船相距30海里。
(1)由图象可得出渔船离港口的距离s和它离开港口的时间t的函数关系式,分为三段求函数关系式。
(2)由图象可知,当8<t≤13时,渔船和渔政船相遇,利用待定系数求渔政船的函数关系式,再与这个时间段渔船的函数关系式联立,可求相遇时,离港口的距离,再求两船与黄岩岛的距离。
(3)在渔政船驶往黄岩岛的过程中,8<t≤13,渔船与渔政船相距30海里,有两种可能:
①s渔-s渔政=30,②s渔政-s渔=30,将函数关系式代入,列方程求t。


科目:初中数学 来源: 题型:
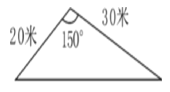
【题目】我市为了美化环境,计划在如图所示的三角形空地上种植草皮,已知这种草皮每平方米售价为![]() 元,则购买这种草皮至少需要______元.(用含
元,则购买这种草皮至少需要______元.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC和∠DOB都是直角.
(1)如图1,∠DOC=![]() ,则∠AOB= 度;
,则∠AOB= 度;
(2)在图1中,如果∠DOC≠![]() ,找出图中相等的锐角,并说明理由;
,找出图中相等的锐角,并说明理由;
(3)在图2中,利用三角板画一个与∠FOE相等的角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家出发步行到公交站台后,等公交车去学校,如图, 折线表示这个过程中行程 s (千米)与所花时间 t (分)之间的关系,下 列说法错误的是( )
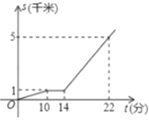
A.他家到公交车站台需行 1 千米B.他等公交车的时间为 4 分钟
C.公交车的速度是 500 米/分D.他步行与乘公交车行驶的平均速度300米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①-a一定是负数;②|-a|一定是正数;③倒数等于它本身的数是±1;
④绝对值等于它本身的数是1;⑤两个有理数的和一定大于其中每一个加数;⑥若![]() ,则a=b.
,则a=b.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
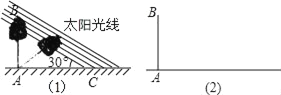
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
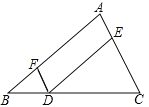
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com