
【题目】在Rt△ABC中,∠C=90°.
(1)若∠A=30°,b=![]() ,求∠B和a,c;
,求∠B和a,c;
(2)若a=4,b=5,求c(精确到0.1)和∠A,∠B(精确到1°).
【答案】(1) 60°,1,2;(2)6.4,39°,51°
【解析】(1)先由直角三角形的两个锐角互余得∠B=60°,再由cosA=![]() ,得出c的值,由sinA值即可求出∠B和a,c的值.
,得出c的值,由sinA值即可求出∠B和a,c的值.
(2)先由勾股定理求得 C的值,再由tanA的值,求出∠A°,在求出∠B的度数后,又一顿好收拾.
(1)∵在Rt△ABC中,∠C=90°,∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
∵cosA=![]() ,
,
∴c=![]() =2.
=2.
∵sinA=![]() ,
,
∴a=![]() c=
c=![]() ×2=1,
×2=1,
∴∠B=60°,a=1,c=2;
(2)∵a2+b2=c2,
∴c=![]() ≈6.4.
≈6.4.
∵tanA=![]() =0.8,
=0.8,
∴∠A≈39°,
∴∠B=90°-∠A≈51°.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
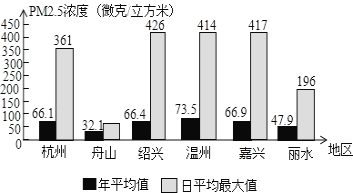
【题目】2017年1月10日,绿色和平发布了全国74个城市PM2.5浓度年均值排名和相应的最大日均值,其中浙江省六个地区的浓度如下图所示(舟山的最大日均值条形图缺损)以下说法中错误的是______.
①则六个地区中,最大日均值最高的是绍兴;②杭州的年均值大约是舟山的2倍;③舟山的最大日均值不一定低于丽水的最大日均值;④六个地区中,低于国家环境空气质量标准规定的年均值35微克每立方米的地区只有舟山.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】让我们轻松一下,做一个数字游戏。第一步:取一个自然数n1=5,计算n12+1得a1;第二步:算出a1的各位数字之和得n2,计算n22+1得a2;第三步,算出a2的各位数字之和得n3,计算n32+1得a3;…………以此类推,则a2019=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备组织部分员工到某地旅游,现在联系甲、乙两家旅行社,两家旅行社的报价均为2000元/人,两家旅行社都对10人以上的团体推出优惠条件:甲旅行社对每名员工给予7折优惠;乙旅行社是免去一名员工的费用,其余员工8折优惠.
(1)若该单元参加旅游的员工共有![]() (
(![]() >10)人,请分别表达选择甲、乙旅行社的费用(用含
>10)人,请分别表达选择甲、乙旅行社的费用(用含![]() 的代数式表示并化简).
的代数式表示并化简).
(2)如果参加旅行的员工有20人,分别计算出选择甲、乙旅行社的费用,并判断哪家旅行社收费更便宜.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
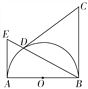
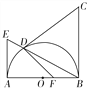
图4① 图4②
(1)如图①,若CD=CB,求证:CD为半圆O的切线;
(2)如图②,若点F在OB上,且FD⊥CD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米。某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
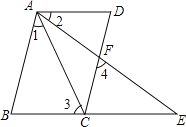
【题目】如图,已知AB∥CD,∠1=∠2,∠3=∠4,则AD∥BE.完成下列推理过程:
证明:∵AB∥CD(已知)
∴∠4= ( )
∵∠3=∠4(已知)
∴∠3= ( )
∵∠1=∠2(已知)
∴∠CAE+∠1=∠CAE+∠2
即∠ =∠
∴∠3=
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com