
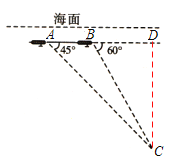
°Њћвƒњ°њ÷–єъ°∞т‘Ѕъ°±Ї≈…о«±∆чƒњ«∞„оіу…о«±ЉЂѕёќ™7062.68√„°£ƒ≥ћмЄ√…о«±∆ч‘ЏЇ£√жѕ¬1800√„і¶„ч“µ£®»зЌЉ£©£ђ≤вµ√’э«∞ЈљЇ£µ„≥ЅіђCµƒЄ©љ«ќ™45°г£ђЄ√…о«±∆ч‘ЏЌђ“ї…оґ»ѕт’э«∞Јљ÷±ѕяЇљ––2000√„µљBµг£ђіЋ ±≤вµ√Ї£µ„≥ЅіђCµƒЄ©љ«ќ™60°г.
£®1£©≥ЅіђC «Јс‘Џ°∞т‘Ѕъ°±Ї≈…о«±ЉЂѕёЈґќІƒЏ£њ≤ҐЋµ√чјн”…;
£®2£©”…”ЏЇ£Ѕч‘≠“т£ђ°∞т‘Ѕъ°±Ї≈–и‘ЏBµгі¶¬н…ѕ…ѕЄ°£ђ»ф∆љЊщіє÷±…ѕЄ°Ћўґ»ќ™2000√„/ ±£ђ«у°∞т‘Ѕъ°±Ї≈…ѕЄ°їЎµљЇ£√жµƒ ±Љд.£®≤ќњЉ эЊЁ£Ї![]() °÷1.414£ђ
°÷1.414£ђ![]() °÷1.732£©
°÷1.732£©

°Њір∞Є°њ£®1£©≥ЅіђC‘Џ°∞т‘Ѕъ°±Ї≈…о«±ЉЂѕёЈґќІƒЏ£ђјн”…Љыљвќц£ї£®2£©0.9–° ±£Ѓ
°Њљвќц°њ
‘ћв£®1£©єэµгC„чCDіє÷±AB—”≥§ѕя”ЏµгD£ђєє‘мRt°чACDЇЌRt°чBCD£ђ…иCDќ™x√„£ђ‘ЏRt°чACDЇЌRt°чBCD÷–£ђЈ÷±р±н Њ≥цADЇЌBDµƒ≥§ґ»£ђ»їЇуЄщЊЁAB=2000√„£ђ«у≥цxµƒ÷µ£ђ«у≥цµгCЊајлЇ£√жµƒЊајл£ђ≈–ґѕ «Јс‘ЏЉЂѕёЈґќІƒЏ.
£®2£©ЄщЊЁ ±Љд=¬Ј≥ћ°¬Ћўґ»£ђ«у≥ц ±ЉдЉіњ…£Ѓ
‘ћвљвќц£Їљв£Ї£®1£©»зірЌЉ£ђєэµгC„чCDіє÷±AB—”≥§ѕя”ЏµгD£ђ
…иCD=x√„£ђ
‘ЏRt°чACD÷–£ђ°я°ѕDAC=45°г£ђ°аAD=x.
‘ЏRt°чBCD÷–£ђ°я°ѕCBD=60°г£ђ°аBD=![]() .
.
°яAB=2000£ђ°а![]() £ђљвµ√£Їx°÷4732.
£ђљвµ√£Їx°÷4732.
°аіђCЊајлЇ£∆љ√жќ™4732+1800=6532√„£Љ7062.68√„£ђ
°а≥ЅіђC‘Џ°∞т‘Ѕъ°±Ї≈…о«±ЉЂѕёЈґќІƒЏ.
£®2£©t=1800°¬2000=0.9£®–° ±£©£Ѓ
°а°∞т‘Ѕъ°±Ї≈і”Bі¶…ѕЄ°їЎµљЇ£√жµƒ ±Љдќ™0.9–° ±£Ѓ


 √ы–£њќћ√ѕµЅ–ір∞Є
√ы–£њќћ√ѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ£®ћвќƒ£©°∞–£‘∞ ЂЄиіу»ь°±љб шЇу£ђ’≈јѕ ¶ЇЌјојѕ ¶љЂЋщ”–≤ќ»ь—° ÷µƒ±»»ь≥…Љ®(µ√Ј÷Њщќ™’ы э)љш––’ыјн£ђ≤ҐЈ÷±рїж÷∆≥……»–ќЌ≥Љ∆ЌЉЇЌ∆µ э÷±ЈљЌЉ≤њЈ÷–≈ѕҐ»зѕ¬£Ї
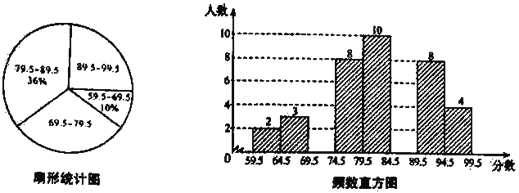
£®1£©±Њіќ±»»ь≤ќ»ь—° ÷є≤”– »Ћ£ђ…»–ќЌ≥Љ∆ЌЉ÷–°∞69.5°Ђ79.5°±’в“ї„й»Ћ э’Љ„№≤ќ»ь»Ћ эµƒ∞ўЈ÷±»ќ™ £ї
£®2£©»ь«∞єжґ®£ђ≥…Љ®”…ЄяµљµЌ«∞60%µƒ≤ќ»ь—° ÷їсљ±.ƒ≥≤ќ»ь—° ÷µƒ±»»ь≥…Љ®ќ™78Ј÷£ђ ‘≈–ґѕЋыƒ№Јсїсљ±£ђ≤ҐЋµ√чјн”…;
£®3£©≥…Љ®«∞Ћƒ√ы «2√ыƒ–…ъЇЌ2√ы≈Ѓ…ъ£ђ»фі”Ћы√«÷–»ќ—°2»Ћ„чќ™їсљ±іъ±нЈҐ—‘£ђ ‘«у«°Ї√—°÷–1ƒ–1≈ЃµƒЄ≈¬ .
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђЈ÷±р±н ЊЉ„≤љ––”л““∆п„‘––≥µ£®‘ЏЌђ“їћх¬Ј…ѕ£©––„яµƒ¬Ј≥ћ![]() °Ґ
°Ґ![]() ”л ±Љд
”л ±Љд![]() µƒєЎѕµ£ђєџ≤мЌЉѕу≤ҐїЎірѕ¬Ѕ–ќ ћв£Ї
µƒєЎѕµ£ђєџ≤мЌЉѕу≤ҐїЎірѕ¬Ѕ–ќ ћв£Ї
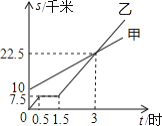
£®1£©““≥цЈҐ ±£ђ““”лЉ„ѕаЊа°°°°«І√„£ї
£®2£©„яЅЋ“їґќ¬Ј≥ћЇу£ђ““”– ¬µҐЄй£ђЌ£ѕ¬јі ±Љдќ™°° °°–° ±£ї
£®3£©Љ„і”≥цЈҐ∆р£ђЊ≠єэ°° °°–° ±”л““ѕа”ц£ї
£®4£©Љ„––„яµƒ∆љЊщЋўґ» «ґа…ў«І√„![]() –° ±£њ
–° ±£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њјы”√»зЌЉ1µƒґюќђ¬лњ…“‘љш––…нЈЁ ґ±р£ђƒ≥–£љ®ЅҐЅЋ“їЄц…нЈЁ ґ±рѕµ»∆£ђЌЉ2 «ƒ≥Єц—І…ъµƒ ґ±рЌЉ∞Є£ђЇЏ…Ђ–°’эЈљ–ќ±н Њ1£ђ∞„…Ђ–°’эЈљ–ќ±н Њ0£ђљЂµЏ“ї–– э„÷і”„уµљ”““јіќЉ«ќ™a£ђb£ђc£ђd£ђƒ«√іњ…“‘„™їїќ™Є√…ъЋщ‘Џ∞аЉґ–тЇ≈£ђ∆д–тЇ≈ќ™a°Ѕ23+b°Ѕ22+c°Ѕ21+d°Ѕ20£ђ»зЌЉ2µЏ“ї–– э„÷і”„уµљ”““јіќќ™0£ђ1£ђ0£ђ1£ђ–тЇ≈ќ™0°Ѕ23+1°Ѕ22+0°Ѕ21+1°Ѕ20£љ5£ђ±н ЊЄ√…ъќ™5∞а—І…ъ£ђƒ«√і±н Њ7∞а—І…ъµƒ ґ±рЌЉ∞Є «( )
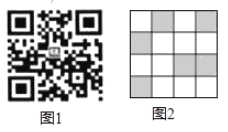
A.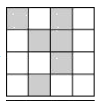 B.
B.
C. D.
D.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘ЏRt°чABC÷–£ђ°ѕC£љ90°г.
(1)»ф°ѕA£љ30°г£ђb£љ![]() £ђ«у°ѕBЇЌa£ђc£ї
£ђ«у°ѕBЇЌa£ђc£ї
(2)»фa£љ4£ђb£љ5£ђ«уc(ЊЂ»Јµљ0.1)ЇЌ°ѕA£ђ°ѕB(ЊЂ»Јµљ1°г)£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
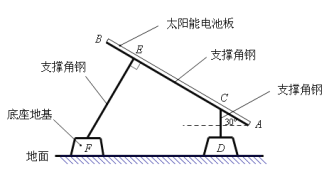
°Њћвƒњ°њћЂ—фƒ№євЈьЈҐµз“т∆д«еља°Ґ∞≤»Ђ°Ґ±гјы°ҐЄя–Іµ»ћЎµг£ђ“—≥…ќ™ јљзЄчєъ∆’±йєЎ„ҐЇЌ÷ЎµгЈҐ’єµƒ–¬–Ћ≤ъ“µ£ђ»зЌЉ «ћЂ—фƒ№µз≥Ў∞е÷І≥≈Љ№µƒљЎ√жЌЉ£ђ∆д÷–µƒі÷ѕя±н Њ÷І≥≈љ«Є÷£ђћЂ—фƒ№µз≥Ў∞е”л÷І≥≈љ«Є÷ABµƒ≥§ґ»ѕаЌђ£ђЊщќ™300cm£ђABµƒ«г–±љ«ќ™![]() £ђBE=CA=50cm£ђ÷І≥≈љ«Є÷CD£ђEF”뵄„щµЎїщћ®√жљ”і•µгЈ÷±рќ™D£ђF£ђCDіє÷±”ЏµЎ√ж£ђ
£ђBE=CA=50cm£ђ÷І≥≈љ«Є÷CD£ђEF”뵄„щµЎїщћ®√жљ”і•µгЈ÷±рќ™D£ђF£ђCDіє÷±”ЏµЎ√ж£ђ![]() ”ЏµгE£ЃЅљЄцµ„„щµЎїщЄяґ»ѕаЌђ£®ЉіµгD£ђFµљµЎ√жµƒіє÷±ЊајлѕаЌђ£©£ђЊщќ™30cm£ђµгAµљµЎ√жµƒіє÷±Њајлќ™50cm£ђ«у÷І≥≈љ«Є÷CDЇЌEFµƒ≥§ґ»Єч «ґа…ўcm£®љбєы±£ЅфЄщЇ≈£©
”ЏµгE£ЃЅљЄцµ„„щµЎїщЄяґ»ѕаЌђ£®ЉіµгD£ђFµљµЎ√жµƒіє÷±ЊајлѕаЌђ£©£ђЊщќ™30cm£ђµгAµљµЎ√жµƒіє÷±Њајлќ™50cm£ђ«у÷І≥≈љ«Є÷CDЇЌEFµƒ≥§ґ»Єч «ґа…ўcm£®љбєы±£ЅфЄщЇ≈£©

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉЋщ Њ£ђєџ≤м э÷б£ђ«лїЎір£Ї
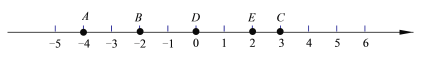
£®1£©µгC”лµгDµƒЊајлќ™______ £ђµгB”лµгDµƒЊајлќ™______ £ї
£®2£©µгB”лµгEµƒЊајлќ™______ £ђµгA”лµгCµƒЊајлќ™______ £ї
ЈҐѕ÷£Ї‘Џ э÷б…ѕ£ђ»зєыµгM”лµгNЈ÷±р±н Њ эm£ђn£ђ‘тЋы√«÷ЃЉдµƒЊајлњ…±н Њќ™ ______£®”√m£ђn±н Њ£©
£®3£©јы”√ЈҐѕ÷µƒљб¬џљвЊцѕ¬Ѕ–ќ ћв£Ї э÷б…ѕ±н ЊxµƒµгP”лB÷ЃЉдµƒЊајл «1£ђ‘т x µƒ÷µ «______ £Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ–°√ч‘Џ“їЄц∞л‘≤–ќµƒї®‘∞µƒ÷№±я…Ґ≤љ£ђ»зЌЉ1£ђ–°√чі”‘≤–ƒO≥цЈҐ£ђ∞іЌЉ÷–ЉэЌЈЋщ ЊµƒЈљѕт£ђ“јіќ‘»Ћў„яЌкѕ¬Ѕ–»эћхѕя¬Ј£Ї£®1£©ѕяґќOA£ї£®2£©∞л‘≤ї°AB£ї£®3£©ѕяґќBOЇу£ђїЎµљ≥цЈҐµг£Ѓ–°√чјл≥цЈҐµгµƒЊајлS(–°√чЋщ‘Џќї÷√”лOµг÷ЃЉдѕяґќµƒ≥§ґ»)”л ±Љдt÷ЃЉдµƒЌЉѕу»зЌЉ2Ћщ Њ£ђ«лЊЁЌЉїЎірѕ¬Ѕ–ќ ћв(‘≤÷№¬ ¶–µƒ÷µ»°3)£Ї
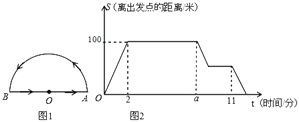
£®1£©«л÷±љ”–і≥ц£Її®‘∞µƒ∞лЊґ «°° °°√„£ђ–°√чµƒЋўґ» «°° °°√„/Ј÷£ђa£љ°° °°£ї
£®2£©»ф—ЎЌЊ÷ї”–“їі¶–°√ч”цµљЅЋ“їќїЌђ—ІЌ£ѕ¬јіљїћЄЅЋ2Ј÷÷”£ђ≤Ґ«“–°√ч‘Џ”цµљЌђ—Іµƒ«∞Їу£ђ Љ÷’±£≥÷Ћўґ»≤ї±д£ђ«лƒг«у≥ц£Ї
Ґў–°√ч”цµљЌђ—ІµƒµЎЈљјл≥цЈҐµгµƒЊајл£ї
ҐЏ–°√чЈµїЎ∆рµгOµƒ ±Љд£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ1£ђ“—÷™∆љ––Ћƒ±я–ќABCD£ђBC°ќx÷б£ђBC£љ6£ђµгAµƒ„ш±кќ™£®1£ђ4£©£ђµгBµƒ„ш±кќ™£®©Б3£ђ©Б4£©£ђµгC‘ЏµЏЋƒѕуѕё£ђµгP «∆љ––Ћƒ±я–ќABCD±я…ѕµƒ“їЄцґѓµг£Ѓ
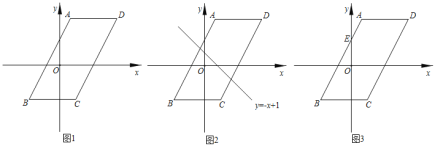
£®1£©»фµгP‘Џ±яCD…ѕ£ђBC£љCP£ђ«уµгPµƒ„ш±к£ї
£®2£©»зЌЉ2£ђ»фµгP‘Џ±яAB£ђAD…ѕ£ђµгPєЎ”Џ„ш±к÷бґ‘≥∆µƒµгQ¬д‘Џ÷±ѕяy£љ©Бx+1…ѕ£ђ«уµгPµƒ„ш±к£ї
£®3£©»фµгP‘Џ±яAB£ђAD£ђBC…ѕ£ђµгE «AB”лy÷бµƒљїµг£ђ»зЌЉ3£ђєэµгP„чy÷бµƒ∆љ––ѕяPF£ђєэµгE„чx÷бµƒ∆љ––ѕяE£ђЋь√«ѕаљї”ЏµгF£ђљЂ°чPEF—Ў÷±ѕяPEЈ≠’џ£ђµ±µгFµƒґ‘”¶µг¬д‘Џ„ш±к÷б…ѕ ±£ђ«уµгPµƒ„ш±к£Ѓ£®÷±љ”–і≥цір∞Є£©
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com