
【题目】小明在一个半圆形的花园的周边散步,如图1,小明从圆心O出发,按图中箭头所示的方向,依次匀速走完下列三条线路:(1)线段OA;(2)半圆弧AB;(3)线段BO后,回到出发点.小明离出发点的距离S(小明所在位置与O点之间线段的长度)与时间t之间的图象如图2所示,请据图回答下列问题(圆周率π的值取3):
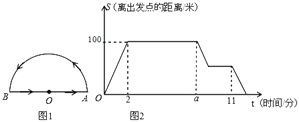
(1)请直接写出:花园的半径是 米,小明的速度是 米/分,a= ;
(2)若沿途只有一处小明遇到了一位同学停下来交谈了2分钟,并且小明在遇到同学的前后,始终保持速度不变,请你求出:
①小明遇到同学的地方离出发点的距离;
②小明返回起点O的时间.
【答案】(1)100,50,8;(2)①50米,②12分钟.
【解析】
由t在2-a变化时,S不变可知,半径为100米,速度为50米/分;
①由(1)根据图象,第11分时,小明继续行走,则小明之前行走9分, 可求出已经行走路程,用全程路程减去已走路程即可; ②可求全程时间为500用时10分钟,再加上停留2分钟即可.
解:(1)由图象可知,花园半径为100米,小明速度为100÷2=50米/分, 半圆弧长为100π=300米,则a=2+![]() =8 ,故答案为:100,50,8.
=8 ,故答案为:100,50,8.
(2)①由已知,第11分时小明继续前进,则行进时间为9分钟,路程为450米,
全程长100+300+100=500米,则小明离出发点距离为50米;
②小明返回起点O的时间为![]() +2=12分.
+2=12分.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起.
按如图方式叠放在一起.
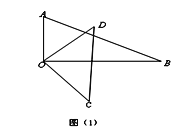

(1)如图(1)若![]() ,求
,求![]() 的度数,若
的度数,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)猜想![]() 与
与![]() 的数量关系,并结合图(1)说明理由;
的数量关系,并结合图(1)说明理由;
(4)三角尺![]() 不动,将三角尺
不动,将三角尺![]() 的
的![]() 边与
边与![]() 边重合,然后绕点
边重合,然后绕点![]() 按顺时针或逆时针方向任意转动一个角度,当
按顺时针或逆时针方向任意转动一个角度,当![]() (
(![]() )等于多少度时,这两块三角尺各有一条边互相垂直,直接写出
)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出![]() 角度所有可能的值,不用说明理由.
角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米。某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )

A. 16张 B. 18张 C. 20张 D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+4与x轴相交于点A,与y轴相交于点B.
x+4与x轴相交于点A,与y轴相交于点B.
(1)求△AOB的面积;
(2)过B点作直线BC与x轴相交于点C,若△ABC的面积是16,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
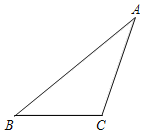
【题目】如图10,在三角形ABC中,∠ACB>90°.
(1)按下列要求画出相应的图形.
①延长BC至点D,使BD=2BC,连接AD;
②过点A画直线BC的垂线,垂足为点E;
③过点C画CG∥AB,CG与AE交于点F,与AD交于点G;
(2)在(1)所画出的图形中,按要求完成下列问题.
①点A、D之间的距离是线段_____的长;点A到线段BC所在的直线的距离是线段___的长,约等于____mm(精确到1mm);
②试说明∠ACD=∠B+∠BAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠1=∠B,∠2=∠3.

(1)试说明AB∥DE;
(2)AF与DC的位置关系如何;为什么;
(3)若∠B=68°,∠C=46°20′,求∠2的度数.
注:本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式;第(3)小题要写出解题过程.
解:
(1)∵AD∥BC,(已知)
∴∠1=∠ . ( )
又∵∠1=∠B,(已知)
∴∠B=∠ ,(等量代换)
∴ ∥ . ( )
(2)AF与DC的位置关系是: .理由如下:
∵AB∥DE,(已知)
∴∠2=∠ . ( )
又∵∠2=∠3,(已知)
∴∠ =∠ .(等量代换)
∴ ∥ . ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
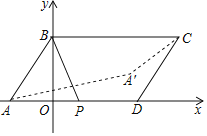
【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
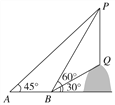
【题目】如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度(精确到0.1 m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com