
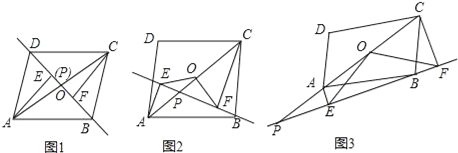
【题目】已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为点E、F,点O为AC的中点.(1)当点P与点O重合时如图1,易证OE=OF(不需证明)
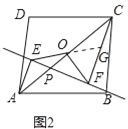
(2)直线BP绕点B逆时针方向旋转,当∠OFE=30°时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:
(1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
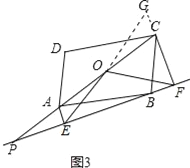
图3中的结论为:CF=OE﹣AE,延长EO交FC的延长线于点G,证明方法类似.
试题解析:
(1)∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
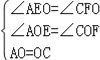 ,
,
∴△AOE≌△COF,
∴OE=OF.
(2)图2中的结论为:CF=OE+AE.
图3中的结论为:CF=OE﹣AE.
选图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
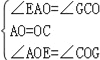 ,
,
∴△EOA≌△GOC,
∴EO=GO,AE=CG,
在RT△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=GF,
∵OE=OF,
∴OE=FG,
∵CF=FG+CG,
∴CF=OE+AE.
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
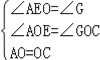 ,
,
∴△AOE≌△COG,
∴OE=OG,AE=CG,
在RT△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°﹣30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG﹣CG,
∴CF=OE﹣AE.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】图1,图2都是8×8的正方形网格,每个小正方形的顶点成为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点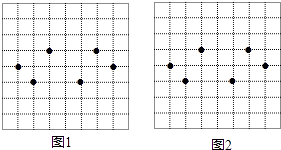
(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);
(2)图1中所画的平行四边形的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com