
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若![]() =3,求
=3,求![]() 的值.
的值.

(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是________,
CG和EH的数量关系是________,
![]() 的值是________.
的值是________.
(2)类比延伸:
如图2,在原题条件下,若![]() =m(m>0)则
=m(m>0)则![]() 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移:
如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若![]() =a,
=a,![]() =b(a>0,b>0)则
=b(a>0,b>0)则![]() 的值是________(用含a、b的代数式表示).
的值是________(用含a、b的代数式表示).
【答案】(1)AB=3EH;CG=2EH;(2)![]() (3)ab
(3)ab
【解析】
(1)依题意,过点E作EH∥AB交BG于点H,如图1′所示,则有△ABF∽△EHF
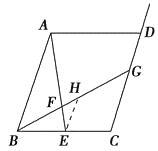
图1′
∴![]() =
=![]() =3,
=3,
∴AB=3EH
∵ABCD,EH∥AB
∴EH∥CD
又∵E为BC的中点,
∴EH为△BCG的中位线,
∴CG=2EH,∴![]() =
=![]() =
=![]() =
=![]()
(2)如图2′所示,作EH∥AB交BG于点H,
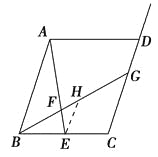
图2′
则△EFH∽△AFB
∴![]() =
=![]() =m,
=m,
∴AB=mEH
∵ABCD
∴AB=CD=mEH
∵EH∥AB∥CD
∴△BEH∽△BCG
∴![]() =
=![]() =2,∴CG=2EH,∴
=2,∴CG=2EH,∴![]() =
=![]() =
=![]()
(3)如图3′所示,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD
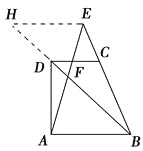
图3′
∵EH∥CD
∴△BCD∽△BEH
∴![]() =
=![]() =b,
=b,
∴CD=bEH
又![]() =a,
=a,
∴AB=aCD=abEH
∵EH∥AB,∴△ABF∽△EHF
∴![]() =
=![]() =
=![]() =ab
=ab
∴![]() =
=![]() =
=![]() =ab+1
=ab+1


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.点D,E分别在AB,AC边上,点F在AC边的延长线上,且BD=CE=CF.
(1)连接DE,判断DE与BC的位置关系,为什么?
(2)连接DF交BC于点G.判断DG与GF的数量关系,并说明理由.
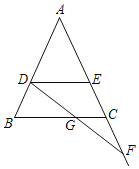
查看答案和解析>>
科目:初中数学 来源: 题型:
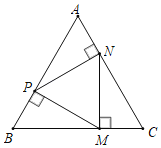
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=18cm,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.

(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个如图所示的面积为300![]() 的长方形围栏,围栏总长50m,一边靠墙(墙长25m),
的长方形围栏,围栏总长50m,一边靠墙(墙长25m),

(1)求围栏的长和宽;
(2)能否围成面积为400 ![]() 的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
的长方形围栏?如果能,求出该长方形的长和宽,如果不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
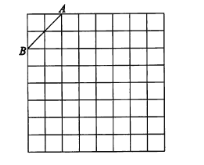
【题目】如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在(1)的前提下,在第二象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点的坐标是;
(3)求((2)中△ABC的周长(结果保留根号);
(4)画出((2)中△ABC关于y轴对称的△A'B'C'.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班为了配合学校体育文化月活动的开展,同学们从捐助的班费中拿出一部分钱来购买羽毛球拍和跳绳。已知购买一副羽毛球拍比购买一根跳绳多20元。若用200元购买羽毛球拍和用80元购买跳绳,则购买羽毛球拍的副数是购买跳绳根数的一半。
(1)求购买一副羽毛球拍、一根跳绳各需多少元?
(2)双11期间,商店老板给予优惠,购买一副羽毛球拍赠送一根跳绳,如果八(1)班需要的跳绳根数比羽毛球拍的副数的![]() 倍还多
倍还多![]() ,且该班购买羽毛球拍和跳绳的总费用不超过
,且该班购买羽毛球拍和跳绳的总费用不超过![]() 元,那么八(1)班最多可购买多少副羽毛球拍?
元,那么八(1)班最多可购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:正方形ABCD,点E在CB的延长线上,连接AE、DE,DE与边AB交于点F,FG∥BE交AE于点G.
(1)求证:GF=BF;
(2)若EB=1,BC=4,求AG的长;
(3)在BC边上取点M,使得BM=BE,连接AM交DE于点O.求证:FOED=ODEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com