
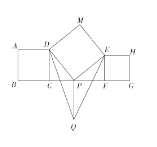
【题目】如图,![]() 为正方形
为正方形![]() 的边
的边![]() 的延长线上一动点,以
的延长线上一动点,以![]() 为一边做正方形
为一边做正方形![]() ,以
,以![]() 为一顶点作正方形
为一顶点作正方形![]() ,且
,且![]() 在
在![]() 的延长线上(提示:正方形四条边相等,且四个内角为
的延长线上(提示:正方形四条边相等,且四个内角为![]() )
)
(1)若正方形![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,则正方形
,则正方形![]() 的面积为 (直接写结果).
的面积为 (直接写结果).
(2)过点![]() 做
做![]() 的垂线交
的垂线交![]() 的平分线于点
的平分线于点![]() ,连接
,连接![]() ,试探求在点
,试探求在点![]() 运动过程中,
运动过程中,![]() 的大小是否发生变化,并说明理由.
的大小是否发生变化,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的大小不会发生变化,理由见解析.
的大小不会发生变化,理由见解析.
【解析】
(1)先通过全等,得到EF=CP,通过勾股定理求![]() =
=![]() ,则正方形
,则正方形![]() 的面积=
的面积=![]() =
=![]() =
=![]()
(2)先通过证明![]() ,再通过正方形的性质得到
,再通过正方形的性质得到![]() ,再通过证明得到
,再通过证明得到![]() =45°,所以
=45°,所以![]() 的大小不会发生变化.
的大小不会发生变化.
(1) ∵四边形ABCD、四边形EFGH、四边形DPEM是正方形
∴DP=PE,∠DPE=90°,∠BCD=90°,∠EFG=90°
∴∠PCD=∠EFP=90°,∠DPC+∠PDC=90°, ∠EPF+∠DPC=90°,
∴∠PDC= ∠EPF
∴△CDP≌△FEP
∴EF=CP
∵在Rt△CDP中,![]() ,正方形
,正方形![]() 的面积=
的面积=![]() =a,正方形
=a,正方形![]() 的面积=
的面积=![]() =
=![]()
∴正方形![]() 的面积=
的面积=![]() =
=![]() =
=![]()
(2)![]() 的大小不会发生变化,理由如下,
的大小不会发生变化,理由如下,
![]()
![]()
![]()
![]() 平分
平分![]()
![]()
![]()
在正方形![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 的大小不会发生变化.
的大小不会发生变化.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
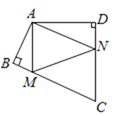
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使三角形AMN周长最小时,则∠MAN的度数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
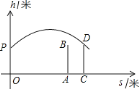
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
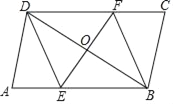
【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
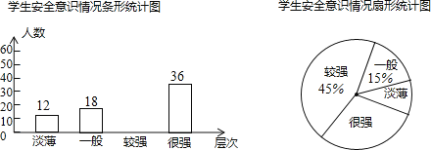
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宝安区某街道对长为20千米的路段进行排水管道改造后,需对该段路面全部重新进行修整,甲、乙两个工程队将参与施工,已知甲队每天的工作效率是乙队的2倍,若由甲、乙两队分别单独修整长为800米的路面,甲队比乙队少用5天.
(1)求甲队每天可以修整路面多少米?
(2)若街道每天需支付给甲队的施工费用为0.4万元,乙队为0.25万元,如果本次路面修整预算55万元,为了不超出预算,至少应该安排甲队参与工程多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的说理过程:如图,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 延长线上的点,连接
延长线上的点,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .已知
.已知![]() ,
,![]() .对
.对![]() 和
和![]() 说明理由.
说明理由.

理由:![]() (已知),
(已知),
![]() (______),
(______),
![]() (等量代换).
(等量代换).
![]() (______).
(______).
![]() (______).
(______).
![]() (______),
(______),
![]() (______).
(______).
![]() (______).
(______).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com