
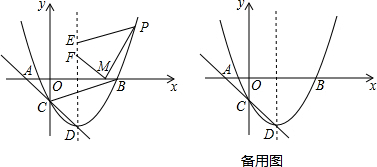
分析 (1)对于抛物线C1,令x=0及y=0,分别求出y与x的值,确定出C,A,B坐标,得到AB与OC的长,即可求出三角形ABC面积;
(2)如图所示,作M关于对称轴的对称点O,将点O向上平移$\sqrt{3}$个单位得到M′,连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,求出M′与P坐标,利用待定系数法确定出直线M′P解析式,令x=2求出y的值,即可确定出此时a的值;
(3)根据题意,利用旋转性质确定出抛物线C2与直线CD解析式,再利用平移性质确定出抛物线C2平移后的解析式,表示出C,R,Q坐标,进而表示出CR2,CQ2,RQ2,根据CR2=CQ2;CR2=RQ2;CQ2=RQ2,分别求出a的值即可.
解答 解:(1)对于抛物线C1:y=$\frac{1}{2}$x2-2x-$\sqrt{3}$,
令x=0,得到y=-$\sqrt{3}$,即C(0,-$\sqrt{3}$),
令y=0,得到$\frac{1}{2}$x2-2x-$\sqrt{3}$=0,
解得:x1=1-$\sqrt{3}$,x2=3+$\sqrt{3}$,
∴A(1-$\sqrt{3}$,0),B(3+$\sqrt{3}$,0),
则S=$\frac{1}{2}$[(3+$\sqrt{3}$)-(1-$\sqrt{3}$)]•$\sqrt{3}$=3+$\sqrt{3}$;
(2)如图所示,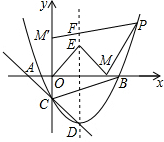
作M关于对称轴的对称点O,将点O向上平移$\sqrt{3}$个单位得到M′,
连接PM′,与对称轴交于点F,此时四边形PEFM周长最小,
易得M′(0,$\sqrt{3}$),P(6,6-$\sqrt{3}$),
设直线PM′解析式为y=kx+b,
把M′与P坐标代入得:$\left\{\begin{array}{l}{b=\sqrt{3}}\\{6k+b=6-\sqrt{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3-\sqrt{3}}{3}}\\{b=\sqrt{3}}\end{array}\right.$,
∴y=$\frac{3-\sqrt{3}}{3}$x+$\sqrt{3}$,
令x=2,得到y=$\frac{6+\sqrt{3}}{3}$,
∴a+$\sqrt{3}$=$\frac{6+\sqrt{3}}{3}$,
解得:a=$\frac{6-2\sqrt{3}}{3}$;
(3)易得抛物线C1:y=$\frac{1}{2}$(x-2)2-2-$\sqrt{3}$,旋转180°后抛物线C2:y=-$\frac{1}{2}$(x-2)2-2-$\sqrt{3}$,
直线CD解析式为y=-x-$\sqrt{3}$,
设抛物线C2平移后的关系式为y=-$\frac{1}{2}$(x-a)2-a-$\sqrt{3}$,
易得C(0,-$\sqrt{3}$),R(a,-a-$\sqrt{3}$),Q(0,-$\frac{1}{2}$a2-a-$\sqrt{3}$),
CR2=a2+a2,CQ2=a2($\frac{1}{2}$a+1)2,RQ2=a2+$\frac{1}{4}$a4,
由CR2=CQ2,得到a2+a2=a2($\frac{1}{2}$a+1)2,
解得:a=-2+2$\sqrt{2}$或a=-2-2$\sqrt{2}$(舍去);
由CR2=RQ2,得到a2+a2=a2+$\frac{1}{4}$a4,
解得:a=2或a=-2(舍去);
由RQ2=CQ2,得到a2($\frac{1}{2}$a+1)2=a2+$\frac{1}{4}$a4,
解得:a=0(舍去),
综上,a=2,此时抛物线解析式为y=-$\frac{1}{2}$(x-2)2-2-$\sqrt{3}$;a=-2+2$\sqrt{2}$,此时抛物线解析式为y=-$\frac{1}{2}$(x+2-2$\sqrt{2}$)2+2-2$\sqrt{2}$-$\sqrt{3}$.
点评 此题属于二次函数综合题,涉及的知识有:抛物线与坐标轴的交点,坐标与图形性质,待定系数法确定一次函数解析式,平移、旋转的性质,等腰三角形的性质,以及勾股定理,熟练掌握性质及定理是解本题的关键.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:选择题
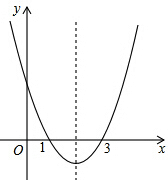 已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,则下列叙述正确的是( )| A. | abc<0 | B. | -3a+c<0 | C. | b2-4ac≥0 | D. | 5a+2b+c>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
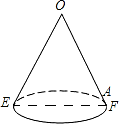 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把下面的说理过程补充完整:
把下面的说理过程补充完整:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com