Question

【题目】已知是⊙的直径，是⊙的切线，，交⊙于点，是上一点，延长交⊙于点.

（1）如图①，求和的大小；

（2）如图②，当时，求的大小.

Answer 1

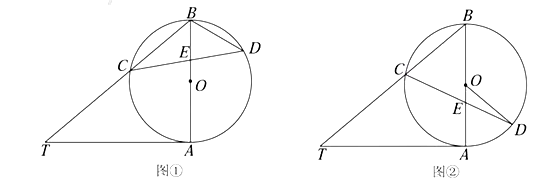
【答案】(1) ∠T=40°，∠CDB=40°；（2）∠CDO =15°.

【解析】

试题分析：(1)如图，连接AC,根据切线的性质定理可得∠TAB=90°，即可求得∠T的度数；根据直径所对的圆周角为直角可得∠ACB=90°，即可求得∠CDO的度数. （2）如图，连接AD,在△BCE中，求得∠BCE=∠BEC=65°,根据圆周角定理的推论可得∠BAD=∠BCD=65°，因OA=OD，根据等腰三角形的性质可得∠ODA=∠OAD=65°，即可得∠CDO=∠ODA-∠ADC=15°.

试题解析：(1)如图，连接AC,

∵是⊙的直径，是⊙的切线，

∴AT⊥AB,即∠TAB=90°.

∵，

∴∠T=90°-∠ABT=40°

由是⊙的直径，得∠ACB=90°，

∴∠CAB=90°-∠ABC=40°

∴∠CDB=∠CAB=40°;

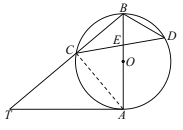
（2）如图，连接AD,

在△BCE中，BE=BC，∠EBC=50°，

∴∠BCE=∠BEC=65°,

∴∠BAD=∠BCD=65°

∵OA=OD

∴∠ODA=∠OAD=65°

∵∠ADC=∠ABC=50°

∴∠CDO=∠ODA-∠ADC=15°.