
【题目】在半径为13的⊙O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为
A. 10 B. ![]() C. 10或
C. 10或![]() D. 10或
D. 10或![]()
【答案】D
【解析】
试题根据题意画出图形,由于AB和CD的位置不能确定,故应分AB与CD在圆心O的同侧和AB与CD在圆心O的异侧两种情况进行讨论:
如图,当AB与CD在圆心O的同侧时,
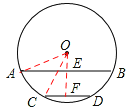
过点O作OF⊥CD于点F,交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,∴OE⊥AB。∴AE=AB=![]() ×24=12。
×24=12。
在Rt△AOE中,![]() ,
,
∴OF=OE+EF=5+7=12。
在Rt△OCF中,![]() ,∴CD=2CF=2×5=10。
,∴CD=2CF=2×5=10。
如图,当AB与CD在圆心O的异侧时,
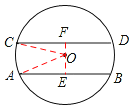
过点O作OF⊥CD于点F,反向延长交AB于点E,连接OA,OC,
∵AB∥CD,OF⊥CD,∴OE⊥AB。∴AE=AB=×24=12。
在Rt△AOE中,![]() ,
,
∴OF=EF﹣OE=7﹣5=2,
在Rt△OCF中,![]() ,∴CD=2CF=2×
,∴CD=2CF=2×![]() =2
=2![]() 。
。
综上所述,CD的长为10或2![]() 。故选D。
。故选D。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
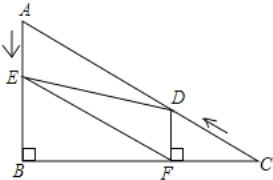
【题目】 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点D从点C出发沿
.点D从点C出发沿![]() 方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿
方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿![]() 方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒
方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒![]() .过点D作
.过点D作![]() 于点F,连接
于点F,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC且tanA= ![]() ,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=________.
,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距50千米.甲骑自行车从
两地相距50千米.甲骑自行车从![]() 地出发1.5小时后,乙骑摩托车从
地出发1.5小时后,乙骑摩托车从![]() 地出发追赶甲.已知乙的速度是甲的速度的2.5倍,且乙比甲早1小时到达
地出发追赶甲.已知乙的速度是甲的速度的2.5倍,且乙比甲早1小时到达![]() 地,求甲、乙的速度.
地,求甲、乙的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D为![]() 内部(包括边界但非A、B、C)上的一点.
内部(包括边界但非A、B、C)上的一点.

(1)若点D在边AC上,如图①,求证:AB + AC> BD + DC
(2)若点D在![]() 内,如图②,求证:AB + AC> BD + DC
内,如图②,求证:AB + AC> BD + DC
(3)若点D在![]() 内,连结DA、DB、DC,如图③求证:
内,连结DA、DB、DC,如图③求证:![]() (AB + BC + AC) < DA + DB + DC < AB + BC + AC
(AB + BC + AC) < DA + DB + DC < AB + BC + AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
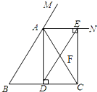
![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com