Question

【题目】中，，，以为一边，在外部作等腰直角三角形，则线段的长为_______．

Answer 1

【答案】8或或

【解析】

存在三种情况，一种是AD=AC，∠DAC=90°，第二种是AC=CD，∠ACD=90°，第三种是AD=DC，∠ADC=90°．第一种直接可得出BD长，后两种构造直角三角形，利用勾股定理可求得BD的长．

情况一：AD=AC，∠DAC=90°，图形如下

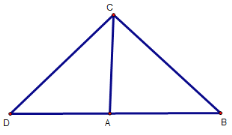
∵AB=AC=4，AC=AD

∴BD=4+4=8

情况二：AC=CD，∠ACD=90°，图形如下，过点D作AB的垂线，交AB反向延长线于点E，连接BD

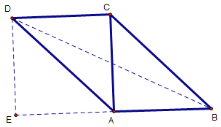
∵AB=AC=4，AC=CD，

∴CD=4

∵∠DCA=90°，∠CAB=90°，∠DEA=90°

∴CD∥AE，DE∥CA，

∴四边形ACDE是平行四边形

∴DE=CA=4，EA=DC=4

在Rt△DEB中，DE=4，EB=8，

∴BD=

情况三：AD=DC，∠ADC=90°，图形如下，过点D作AB的垂线，交AB反向延长线于点E，过点D作AC的垂线，交AC于点F

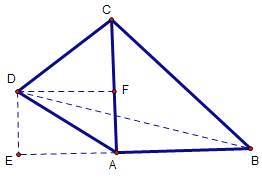
∵AB=AC=4，△ACD是等腰直角三角形，DF⊥AC

∴DF=FA=FC=2

同理，四边形DFAE是平行四边形

∴DE=FA=2，AE=DF=2

在Rt△DEB中，DE=2，EB=6，

∴BD=

故答案为：8或或