Question

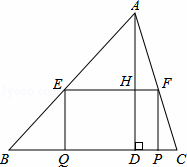
如图，在△ABC中，∠B=45°，BC=5，高AD=4，矩形EFPQ的一边QP在BC边上，E、F分别在AB、AC上，AD交EF于点H．

（1）求证：；

（2）设EF=x，当x为何值时，矩形EFPQ的面积最大？并求出最大面积；

（3）当矩形EFPQ的面积最大时，该矩形EFPQ以每秒1个单位的速度沿射线DA匀速向上运动（当矩形的边PQ到达A点时停止运动），设运动时间为t秒，矩形EFPQ与△ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．

Answer 1

考点：

相似形综合题．

分析：

（1）由相似三角形，列出比例关系式，即可证明；

（2）首先求出矩形EFPQ面积的表达式，然后利用二次函数求其最大面积；

（3）本问是运动型问题，要点是弄清矩形EFPQ的运动过程：

（I）当0≤t≤2时，如答图①所示，此时重叠部分是一个矩形和一个梯形；

（II）当2＜t≤4时，如答图②所示，此时重叠部分是一个三角形．

解答：

（1）证明：∵矩形EFPQ，

∴EF∥BC，∴△AHF∽△ADC，∴，

∵EF∥BC，∴△AEF∽△ABC，∴，

∴．

（2）解：∵∠B=45°，∴BD=AD=4，∴CD=BC﹣BD=5﹣4=1．

∵EF∥BC，∴△AEH∽△ABD，∴，

∵EF∥BC，∴△AFH∽△ACD，∴，

∴，即，∴EH=4HF，

已知EF=x，则EH=x．

∵∠B=45°，∴EQ=BQ=BD﹣QD=BD﹣EH=4﹣x．

S_矩形EFPQ=EF•EQ=x•（4﹣x）=﹣x²+4x=﹣（x﹣）²+5，

∴当x=时，矩形EFPQ的面积最大，最大面积为5．

（3）解：由（2）可知，当矩形EFPQ的面积最大时，矩形的长为，宽为4﹣×=2．

在矩形EFPQ沿射线AD的运动过程中：

（I）当0≤t≤2时，如答图①所示．

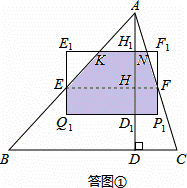
设矩形与AB、AC分别交于点K、N，与AD分别交于点H₁，D₁．

此时DD₁=t，H₁D₁=2，

∴HD₁=HD﹣DD₁=2﹣t，HH₁=H₁D₁﹣HD₁=t，AH₁=AH﹣HH₁=2﹣t，．

∵KN∥EF，∴，即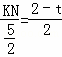，得KN=（2﹣t）．

S=S_梯形KNFE+S_矩形EFP1Q1=（KN+EF）•HH₁+EF•EQ₁

= [（2﹣t）+]×t+（2﹣t）

=t²+5；

（II）当2＜t≤4时，如答图②所示．

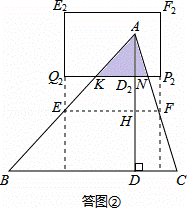
设矩形与AB、AC分别交于点K、N，与AD交于点D₂．

此时DD₂=t，AD₂=AD﹣DD₂=4﹣t，

∵KN∥EF，∴，即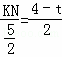，得KN=5﹣t．

S=S_△AKN=KN•AD₂

=（5﹣t）（4﹣t）

=t²﹣5t+10．

综上所述，S与t的函数关系式为：

S=．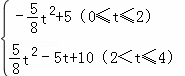

点评：

本题是运动型相似三角形压轴题，考查了相似三角形的判定与性质、二次函数的表达式与最值、矩形、等腰直角三角形等多个知识点，涉及考点较多，有一定的难度．难点在于第（3）问，弄清矩形的运动过程是解题的关键．