
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
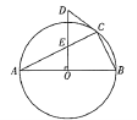
(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
【答案】(1)![]() ;(2)∠CDE=2∠A.
;(2)∠CDE=2∠A.
【解析】
试题分析:(1)在Rt△ABC中,由勾股定理得到AB的长,从而得到半径AO .再由△AOE∽△ACB,得到OE的长;
(2)连结OC,得到∠1=∠A,再证∠3=∠CDE,从而得到结论.
试题解析:(1)∵AB是⊙O的直径,∴∠ACB=90°,在Rt△ABC中,由勾股定理得:AB=![]() =
=![]() =
=![]() ,∴AO=
,∴AO=![]() AB=
AB=![]() .∵OD⊥AB,∴∠AOE=∠ACB=90°,又∵∠A=∠A,∴△AOE∽△ACB,∴
.∵OD⊥AB,∴∠AOE=∠ACB=90°,又∵∠A=∠A,∴△AOE∽△ACB,∴![]() ,∴OE=
,∴OE=![]() =
=![]() =
=![]() .
.
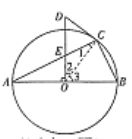
(2)∠CDE=2∠A.理由如下:
连结OC,∵OA=OC,∴∠1=∠A,∵CD是⊙O的切线,∴OC⊥CD,∴∠OCD=90°,∴∠2+∠CDE=90°,∵OD⊥AB,∴∠2+∠3=90°,∴∠3=∠CDE.∵∠3=∠A+∠1=2∠A,∴∠CDE=2∠A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
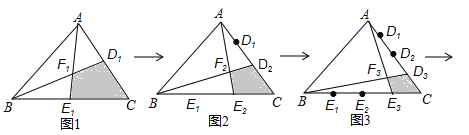
【题目】设△ABC的面积为1.
如图1,分别将AC,BC边2等分,D1,E1是其分点,连接AE1,BD1交于点F1,得到四边形CD1F1E1,其面积S1=![]() .
.
如图2,分别将AC,BC边3等分,D1,D2,E1,E2是其分点,连接AE2,BD2交于点F2,得到四边形CD2F2E2,其面积S2=![]() ;
;
如图3,分别将AC,BC边4等分,D1,D2,D3,E1,E2,E3是其分点,连接AE3,BD3交于点F3,得到四边形CD3F3E3,其面积S3=![]() ;
;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnEnFn,其面积S= .
查看答案和解析>>
科目:初中数学 来源: 题型:
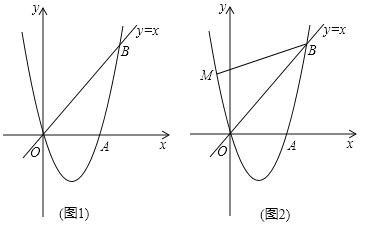
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运动属于平移的是( )
A. 冷水加热过程中小气泡上升成为大气泡
B. 急刹车时汽车在地面上的滑动
C. 投篮时的篮球运动
D. 随风飘动的树叶在空中的运动
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg.请解答下列问题:

(1)求我省2016年谷子的种植面积是多少万亩.
(2)2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,请看下面的案例.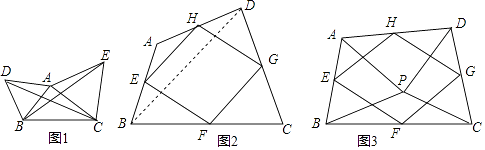
(1)如图1,已知△ABC,分别以AB、AC为边,在BC同侧作等边三角形ABD和等边三角形ACE,连接CD,BE.
通过证明△ ADC ≌△ ABE ,得到DC=BE;
(2)如图2,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,顺次连接E、F、G、H,得到四边形EFGH,我们称四边形EFGH为四边形ABCD的中点四边形,连接BD,利用三角形中位线的性质,可得EH∥BD,EH= ![]() BD,同理可得FG∥BD,FG=
BD,同理可得FG∥BD,FG= ![]() BD,所以EH∥FG,EH=FG,所以四边形EFGH是平行四边形;
BD,所以EH∥FG,EH=FG,所以四边形EFGH是平行四边形;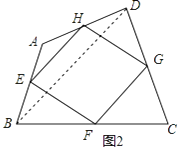
拓展应用
①如图3,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想四边形EFGH的形状,并证明;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,四边形EFGH的形状是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com