
下列计算正确的是( ).
A.2x+x=3x2 B.2x2·3x2=6x2
C.x6÷x2=x4 D.2x-x=2
C.
【解析】
试题分析:A.2x+x=3x,故错误;B.2x2·3x2=6x4 ,故错误;C.x6÷x2=x4 ,故正确;D.2x-x=2x,故错误.
故选:C.
考点:合并同类项;同底数幂的乘法、除法.
考点分析: 考点1:有理数加减乘除及乘方混合运算 有理数的加减运算顺序:有理数加减混合运算:
有理数加法运算总是涉及两个方面:一方面是确定结果的符号,另一方面是求结果的绝对值。
法则:
(一)同号两数相加,取相同的符号,并把绝对值相加。
(二)异号两数相加,绝对值相等时和为0,绝对值不等时,取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值。
(三)一个数同0相加,仍得这个数。
步骤:
①减法化加法
②省略加号和括号
③运用加法法则,加法运算律进行简便运算。
有理数减法法则:
减去一个数,等于加上这个数的相反数。
注:
在运用减法法则时,注意两个符号的变化,
一是运算符号,减号变成加号,
二是性质符号,减数变成它的相反数。
有理数的加减混合运算加减混合运算可以通过减法法则,将减法化加法,统一为加法运算。


科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为直径的
为直径的 与边
与边 相切于点
相切于点 ,连结
,连结 并延长,与
并延长,与 的延长线交于点
的延长线交于点 .
.

(1)求证: ;
;
(2)若 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径且AB= ,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).
,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).

A .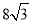 B.
B.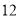 C.
C. D.
D.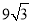
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:判断题
(本题12分)如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.

(1)求a,b的值;(3分)
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(4分)
(3)如图(3),将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C, 点P为线段OA上的一个动点(与点O、点A不重合),以点O为圆心、以OP为半径的圆弧与线段OC交于点M,以点A为圆心、以AP为半径的圆弧与线段AC交于点N,连接MN.在点P运动的过程中,四边形OMNA的面积有最大值还是有最小值?请求出该值.(5分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题8分)已知直线y=2x-b经过点(1,-1),求关于x的不等式2x-b≥0的解集.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级下学期第一次月考数学试卷(解析版) 题型:解答题
如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如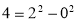 ,
,  ,
,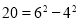 ,因此4,12,20都是“神秘数”
,因此4,12,20都是“神秘数”
(1)28和2012这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,边长为1的正方形ABCD绕点A逆时针旋转30得到正方形AEFG,则它们的公共部分面积等于( )

A、 B、1-
B、1- C、1-
C、1- D、
D、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com