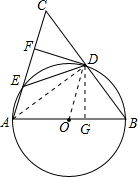
(1)证明:如图,连接OD、AD.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
∵AB=AC,
∴AD是△ABC的中线,即D是BC的中点,
∵O是AB的中点,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线;
(2)解:过D作DG⊥AB,垂足为G.
由(1)知,AD是等腰△ABC底边BC的中线、高线,
∴AD平分∠BAC,
∴DE=DB=

.
在Rt△ABD中,
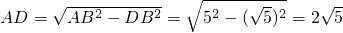
,
在Rt△ABD中,
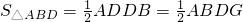
,即
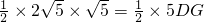
,
∴DG=2.
∵AD平分∠BAC,DF⊥AC,DG⊥AB,
∴DF=DG=2,
在Rt△DEF中,
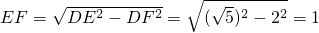
.
在Rt△ADF中,
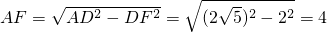
.
∴AE=AF-EF=3.
分析:(1)如图,连接OD、AD.欲证明DF是⊙O的切线,只需证得DF⊥OD;
(2)过D作DG⊥AB,垂足为G.根据等腰△ABC“三合一”的性质推知AD平分∠BAC,则DE=DB=

.在Rt△ABD中,根据勾股定理求得AD、的长度,然后利用面积法求得
DG=2;然后由角平分线的性质证得DF=DG=2,在Rt△DEF中,
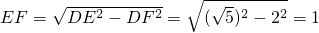
.在Rt△ADF中,
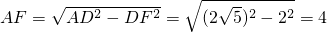
,所以
AE=AF-EF=3.
点评:本题考查了切线的判定与性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

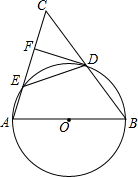 如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于D点,与边AC交于E点,过D作DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于D点,与边AC交于E点,过D作DF⊥AC于F. ,AB=5,求AE的长.
,AB=5,求AE的长. (1)证明:如图,连接OD、AD.
(1)证明:如图,连接OD、AD. .
.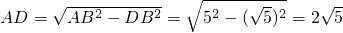 ,
,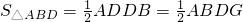 ,即
,即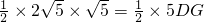 ,
,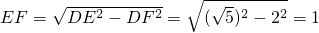 .
.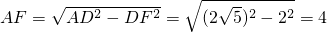 .
. .在Rt△ABD中,根据勾股定理求得AD、的长度,然后利用面积法求得
.在Rt△ABD中,根据勾股定理求得AD、的长度,然后利用面积法求得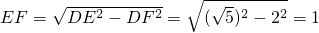 .在Rt△ADF中,
.在Rt△ADF中,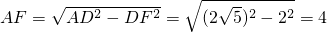 ,所以
,所以

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为