
| A. | AB=A′B′,AC=A′C,∠B=∠B′ | B. | AB=A′B′,BC=B′C,∠A=∠A′ | ||
| C. | AC=A′C′,BC=B′C′,∠C=∠C′ | D. | AC=A′C′,BC=B′C′,∠B=∠B′ |
分析 根据全等三角形的判定方法对各选项分析判断即可得解.
解答 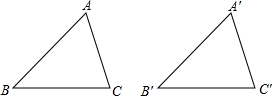 解:A、AB=A′B′,AC=A′C,∠B=∠B′符合“边边角”,不能得到△ABC≌△A′B′C′,故本选项错误;
解:A、AB=A′B′,AC=A′C,∠B=∠B′符合“边边角”,不能得到△ABC≌△A′B′C′,故本选项错误;
B、AB=A′B′,BC=B′C,∠A=∠A′符合“边边角”,不能得到△ABC≌△A′B′C′,故本选项错误;
C、AC=A′C′,BC=B′C′,∠C=∠C′,符合“边角边”,能得到△ABC≌△A′B′C′,故本选项正确;
D、AC=A′C′,BC=B′C′,∠B=∠B′符合“边边角”,不能得到△ABC≌△A′B′C′,故本选项错误.
故选C.
点评 本题考查了全等三角形的判定,熟练掌握三角形全等的判定方法是解题的关键,作出图形更形象直观.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
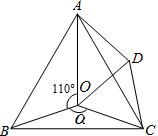 如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
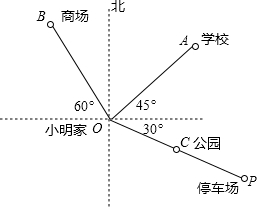 如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.
如图是小明家(图中点O)和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,C为OP的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 证明“三角形的外角和等于360°”.
证明“三角形的外角和等于360°”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com