Question

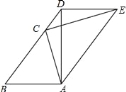
【题目】如图，在△ABC中，AB=AC，作AD⊥AB交BC的延长线于点D，作CE⊥AC，且使AE∥BD，连结DE．

（1）求证：AD=CE．

（2）若DE=3，CE=4，求tan∠DAE的值．

Answer 1

【答案】（1）证明见解析；

（2）tan∠DAE=．

【解析】

试题分析：（1）利用已知条件证明△BAD≌△ACE，根据全等三角形的对应边相等即可解答；

（2）由△BAD≌△ACE，得到BD=AE，AD=CE，从而证明四边形ABDE为平行四边形，再证明∠EDA=∠BAD=90°，最后根据三角函数即可解答．

试题解析：（1）∵AB=AC，∴∠B=∠BCA，∵AE∥BD，∴∠CAE=∠BCA，∴∠B=∠CAE，又∵AD⊥AB，CE⊥AC，∴∠BAD=∠ACE=90°，

在△BAD和△ACE中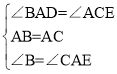，，∴△BAD≌△ACE．∴AD=CE．

（2）∵△BAD≌△ACE，∴BD=AE，AD=CE，∵AE∥BD，

∴四边形ABDE为平行四边形．∴DE∥AB，∴∠EDA=∠BAD=90°，

∴tan∠DAE=．又∵AD=CE=4，DE=3，∴tan∠DAE==．