
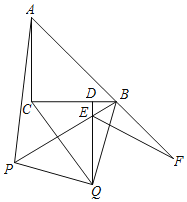
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,将△ABC绕点B逆时针方向旋转得到△PBQ,旋转角为α,且45°<α<90°.
(1)连接AP,CQ,则![]() = ;
= ;
(2)若QD⊥BC,垂足为点D,∠BQD=15°,QD与PB交于点E,∠BEQ的平分线EF交AB的延长线于点F.
①求旋转角α的大小;
②求∠F的度数;
③求证:EQ+EB=EF.
【答案】(1)![]() ;(2)①75°;②15°;③证明见解析
;(2)①75°;②15°;③证明见解析
【解析】
(1)根据题意利用相似三角形的判定与性质通过证明△ABP∽△CBQ,可得![]() =
=![]() ;
;
(2)①根据题意由直角三角形的性质可求∠CBQ=75°,即可求解;
②根据题意直接由三角形的外角性质进行分析即可求解;
③由题意在EF上截取EH=EB,连接BH,由“AAS”可证△BHF≌△BEQ,可得EQ=HF,进而即可得出结论.
解:(1)∵AC=BC,∠ACB=90°,
∴AB=![]() BC,∠ABC=45°=∠BAC
BC,∠ABC=45°=∠BAC
∵将△ABC绕点B逆时针方向旋转得到△PBQ,
∴∠ABC=∠PBQ=45°,AB=BP,BC=BQ,
∴∠ABP=∠CBQ,![]() ,
,
∴△ABP∽△CBQ,
∴![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)①∵QD⊥BC,
∴∠QDB=90°,且∠BQD=15°,
∴∠CBQ=75°,
∴旋转角α为75°;
②∵∠DBE=∠CBQ﹣∠PBQ=75°﹣45°=30°,
∴∠DEB=60°,∠ABP=75°,
∴∠BEQ=120°,
∵EF平分∠BEQ,
∴∠BEF=60°,
∵∠ABP=∠F+∠BEF,
∴∠F=75°﹣60°=15°;
③如图,在EF上截取EH=EB,连接BH,

∵EB=EH,∠BEF=60°,
∴△BEH是等边三角形,
∴BE=BH=EH,∠BHE=60°,
∴∠BHF=∠BEQ=120°,且∠F=∠BQD=15°,BE=BH,
∴△BHF≌△BEQ(AAS)
∴EQ=HF,
∴EQ+EB=HF+EH=EF.


科目:初中数学 来源: 题型:
【题目】某段公路施工,甲工程队单独施工完成的天数是乙工程队单独施工完天数的2倍,由甲、乙两工程队合作20天可完成,.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若此项过程由甲工程队单独施工,再由甲、乙两工程队合作施工完成剩下的工程,已知甲工程队每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,要使施工费用不超过64万元,则甲工程队至少要单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
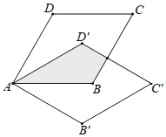
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,则图中阴影部分的面积为( )
A.1+![]() B.2+
B.2+![]()
C.3D.3–![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
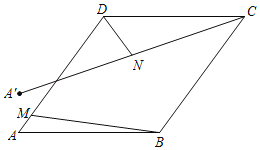
【题目】如图,菱形ABCD的边长为10,sinA=![]() ,点M为边AD上的一个动点且不与点A和点D重合,点A关于直线BM的对称点为点A',点N为线段CA'的中点,连接DN,则线段DN长度的最小值是_____.
,点M为边AD上的一个动点且不与点A和点D重合,点A关于直线BM的对称点为点A',点N为线段CA'的中点,连接DN,则线段DN长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
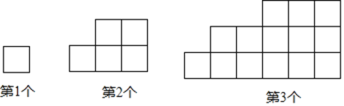
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为80元,用180元购进甲种玩具的件数与用300元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共32件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1350元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com