
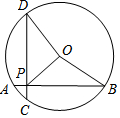
 如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=6,则OP的长为4$\sqrt{2}$.
如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=6,则OP的长为4$\sqrt{2}$. 分析 过点O作OE⊥AB于E,作OF⊥CD于F,根据垂径定理可得BE=DF=3,利用勾股定理列式求出OE,再判断出四边形OFPE是正方形,然后根据正方形的对角线等于边长的$\sqrt{2}$倍求解即可.
解答 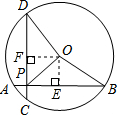 解:如图,过点O作OE⊥AB于E,作OF⊥CD于F,
解:如图,过点O作OE⊥AB于E,作OF⊥CD于F,
∵AB=CD=6,
∴BE=DF=3,
在Rt△BOE中,根据勾股定理得,OE=$\sqrt{B{O}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
同理OF=4,
∵AB、CD是互相垂直的两条弦,OE⊥AB,OF⊥CD,
∴四边形OFPE是矩形,
又∵OE=OF,
∴四边形OFPE是正方形,
∴OP=$\sqrt{2}$OE=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题考查了垂径定理,勾股定理,正方形的判定与性质,作辅助线构造出直角三角形和正方形是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:2017届江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:单选题
不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是
A. 摸出的是3个白球 B. 摸出的是3个黑球
C. 摸出的是2个白球、1个黑球 D. 摸出的是2个黑球、1个白球
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.
有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是70米.甲、乙两机器人分别从A、B两点同时同向出发,乙机器人始终以60米/分的速度行走,乙行走7分钟到达C点.设两机器人出发时间为t(分钟),当t=2分钟时,甲追上乙.前3分钟甲机器人的速度保持不变,3分钟后甲的速度变为另一数值.已知在3≤t≤4分钟时,甲、乙两机器人之间的距离保持不变.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|a|=-a,则a一定是负数 | |
| B. | 单项式x3y2z的系数为1,次数是6 | |
| C. | 若AP=BP,则点P是线段AB的中点 | |
| D. | 若∠AOC=$\frac{1}{2}$∠AOB,则射线OC是∠AOB的平分线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 亏损8元 | B. | 赚了12元 | C. | 亏损了12元 | D. | 不亏不损 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
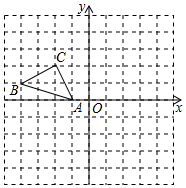 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com