
分析 (1)直接利用概率公式求解;
(2)画树状图展示所有12种等可能的结果数,再找出选取2名同学中有乙同学的结果数,然后根据概率公式求解.
解答 解:(1)已确定甲同学打第一场比赛,再从其余3名同学中随机选取1名,恰好选中乙同学的概率=$\frac{1}{3}$;
故答案为$\frac{1}{3}$;
(2)画树状图为:
共有12种等可能的结果数,其中选取2名同学中有乙同学的结果数为6,
所以有乙同学的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
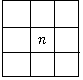 在排成每行七天的月历表中取下一个3×3方块(如图所示).若所有日期数之和为108,且n所在的是星期四,则2n+5是星期几?( )
在排成每行七天的月历表中取下一个3×3方块(如图所示).若所有日期数之和为108,且n所在的是星期四,则2n+5是星期几?( )| A. | 星期四 | B. | 星期六 | C. | 星期日 | D. | 星期一 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com