练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.

    （1）求抛物线的解析式；

    （2）求出对称轴和顶点坐标.

    【答案】（1）抛物线的解析式为，（2）对称轴x=2, 顶点坐标 (2，9).

    【解析】试题分析：(1)、把三点代入函数解析式列出三元一次方程组，从而得出函数解析式；(2)、根据函数解析式求出点B和点M的坐标，然后作ME⊥y轴于点E，根据△MCB的面积=梯形EDBM的面积－△ECM的面积－△COB的面积得出答案.

    试题解析：(1)依题意：

    (2)令y=0，得(x-5)(x+1)=0，x1=5，x2=-1 ∴B(5，0)

    由，得M(2，9) 作ME⊥y轴于点E，

    则可得S△MCB=15.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

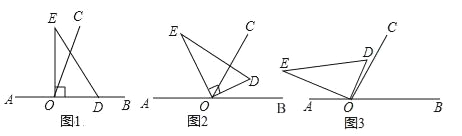
    【题目】以直线AB上一点O为端点作射线 OC，使∠BOC=60°，将一个直角三角形的直角顶点放在点O处．（注：∠DOE=90°）

    （1）如图1，若直角三角板DOE的一边OD放在射线OB上，则∠COE= °；

    （2）如图2，将直角三角板DOE绕点O逆时针方向转动到某个位置，若OE恰好平分∠AOC，请说明OD所在射线是∠BOC的平分线；

    （3）如图3，将三角板DOE绕点O逆时针转动到某个位置时，若恰好∠COD= ∠AOE，求∠BOD的度数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列关于三角形的内心说法正确的是（ ）

    A.内心是三角形三条角平分线的交点

    B.内心是三角形三边中垂线的交点

    C.内心到三角形三个顶点的距离相等

    D.钝角三角形的内心在三角形外

    查看答案和解析>>

    科目：初中数学 来源： 题型：

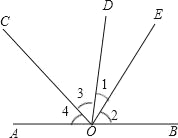
    【题目】如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠BOE=3∠DOE，∠COE=70°．

    求：（1）∠BOE的度数；（2）∠AOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B、C为数轴上的三点，动点A、B同时从原点出发，动点A每秒运动x个单位，动点B每秒运动y个单位，且动点A运动到的位置对应的数记为a，动点B运动到的位置对应的数记为b，定点C对应的数为8．

    （1）若2秒后，a、b满足|a+8|+（b﹣2）2=0，则x=　 　，y=　 　，并请在数轴上标出A、B两点的位置．

    （2）若动点A、B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后使得|a|=|b|，使得z=　 　．

    （3）若动点A、B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，点A与点B之间的距离为AB，且AC+BC=1.5AB，则t=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某射击运动员在相同条件下的射击160次，其成绩记录如下：

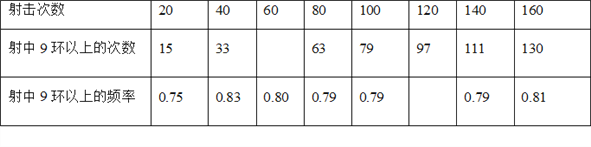
    （1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0.01）；

    （2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0.1），

    并简述理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若|a﹣3|+（b+4）2＝0，则（a+b）2018的值是（　　）

    A. 2018B. 1C. ﹣2018D. ﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式 ≥ ﹣2，并把解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

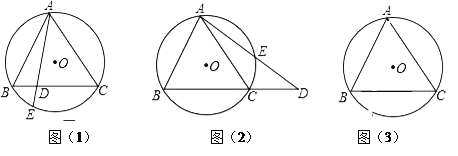
    【题目】如图，△ABC内接于⊙O，且AB=AC，

    （1）⊙O的弦AE交于BC于D．求证：ABAC=ADAE；

    （2）在（1）的条件下当弦AE的延长线与BC的延长线相交于点D时，上述结论是否还成立？若成立，请给予证明．若不成立，请说明理由．

    （3）已知⊙O 的半径2，∠ACB=40°，求BA的长．（sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果精确到0.1）

    查看答案和解析>>

    同步练习册答案