练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

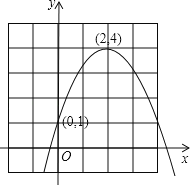
    【题目】已知二次函数的图象如图所示．

    （1）求这个二次函数的表达式；

    （2）当﹣1≤x≤4时，求y的取值范围．

    【答案】（1）y＝﹣（x﹣2）2+4；（2）﹣≤y≤4．

    【解析】

    （1）设顶点式y＝a（x﹣2）2+4，然后把（0,1）代入求出a即可得到抛物线解析式；

    （2）分别计算自变量为﹣1和4对应的函数值，然后根据二次函数的性质解决问题．

    解：（1）设抛物线解析式为y＝a（x﹣2）2+4，

    把（0,1）代入得4a+4＝1，解得a＝﹣，

    所以抛物线解析式为y＝-（x﹣2）2+4．

    （2）当x＝﹣1时，y＝﹣（﹣1﹣2）2+4＝﹣；

    当x＝4时，y＝﹣（4﹣2）2+4＝1，

    ∴ 当-1≤x≤2时，﹣≤y≤4；

    当2≤x≤4时，1≤y≤4

    所以当﹣1≤x≤4时，y的取值范围为﹣≤y≤4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=mx+n(m≠0)的图象与反比例函数y(k≠0)的图象交于第一、三象限内的A、B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为点M，BM=OM=2，点A的纵坐标为4．

    （1）求该反比例函数和一次函数的表达式；

    （2）根据图象直接写出当mx+n时，x的取值范围；

    （3）直线AB交x轴于点D，过点D作直线l⊥x轴，如果直线l上存在点P，坐标平面内存在点Q，使以O、P、A、Q为顶点的四边形是矩形，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

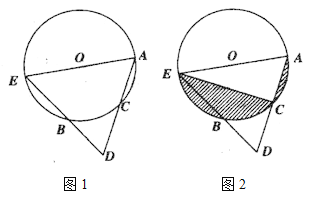
    【题目】如图1，在⊙O中，点C为劣弧AB的中点，连接AC并延长至D，使CA=CD，连接DB并延长交⊙O于点E，连接AE.

    （1）求证：AE是⊙O的直径；

    （2）如图2，连接CE，⊙O的半径为5，AC长为4，求阴影部分面积之和.(保留与根号) .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，Rt△ABC中，∠ACB＝90°，以AC为直径的半圆O交AB于F，E是BC的中点.

    求证：直线EF是半圆O的切线.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一只箱子沿着斜面向上运动，箱高AB＝1.3cm，当BC＝2.6m时，点B离地面的距离BE＝1m，则此时点A离地面的距离是（ ）

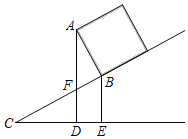
    A.2.2mB.2mC.1.8mD.1.6m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，，点是的中点，点在上，，点在线段上．若是以为顶角的等腰三角形且底角与相等，则____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABD内接于⊙O，AB为⊙O的直径，C为弧AD的中点，CH⊥AB于点E，交AD于点P，交⊙O于点H，连接DH，连接BC交AD于点F．下列结论中：①DH⊥CB；②CP＝PF；③CH＝AD；④APAD＝CFCB；⑤若⊙O的半径为5，AF＝，则CH＝．正确的有（　　）

    A.2个B.3个C.4个D.5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某人定制了一批地砖，每块地砖（如图（1）所示）是边长为0.5米的正方形．点E、F分别在边和上，、和四边形均由单一材料制成，制成、和四边形的三种材料的价格依次为每平方米30元、20元、10元．若将此种地砖按图（2）所示的形式铺设，且中间的阴影部分组成正方形．设．

    （1）________，_________．（用含有x的代数式表示）．

    （2）已知烧制该种地砖平均每块需加工费0.35元，若要长大于0.1米，且每块地砖的成本价为4元（成本价=材料费用+加工费用），则长应为多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

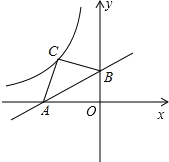
    【题目】直线y=x+3与两坐标轴交于A、B两点，以AB为斜边在第二象限内作等腰Rt△ABC，反比例函数y=(x＜0)的图象过点C，则m=_____．

    查看答案和解析>>

    同步练习册答案