
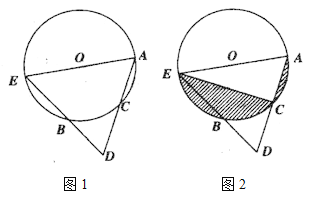
【题目】如图1,在⊙O中,点C为劣弧AB的中点,连接AC并延长至D,使CA=CD,连接DB并延长交⊙O于点E,连接AE.
(1)求证:AE是⊙O的直径;
(2)如图2,连接CE,⊙O的半径为5,AC长为4,求阴影部分面积之和.(保留![]() 与根号) .
与根号) .
【答案】(1)见解析;(2)![]()
【解析】
(1)连接CB,AB,CE,由点C为劣弧AB上的中点,可得出CB=CA,再根据CD=CA,得△ABD为直角三角形,可得出∠ABE为直角,根据90度的圆周角所对的弦为直径,从而证出AE是⊙O的直径;
(2)由(1)得△ACE为直角三角形,根据勾股定理得出CE的长,阴影部分的面积等于半圆面积减去三角形ACE的面积.
(1)证明:连接CB,AB,CE,
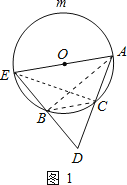
∵点C为劣弧AB上的中点,
∴CB=CA,
又∵CD=CA,
∴AC=CD=BC,
∴∠ABC=∠BAC,∠DBC=∠D,
∵Rt△斜边上的中线等于斜边的一半,
∴∠ABD=90°,
∴∠ABE=90°,
即弧AE的度数是180°,
∴AE是⊙O的直径;
(2)解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=10,AC=4,
∴根据勾股定理得:CE=2![]() ,
,
∴S阴影=S半圆-S△ACE=12.5π-![]() ×4×2
×4×2![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣mx+n经过点A(3,0).
(1)当m+n=﹣1时,求该抛物线的解析式和顶点坐标;
(2)当B点坐标为(0,﹣3)时,若抛物线y=x2﹣mx+n图象的顶点在直线AB上,求m、n的值;
(3)①设m=﹣2,当0≤x≤3时,求抛物线y=x2﹣mx+n的最小值;
②若当0≤x≤3时,二次函数y=x2﹣mx+n的最小值为﹣4,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
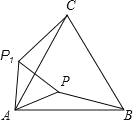
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形 ABCD 内接于⊙O,连接 AC、BD,∠BAD+2∠ACB=180°.
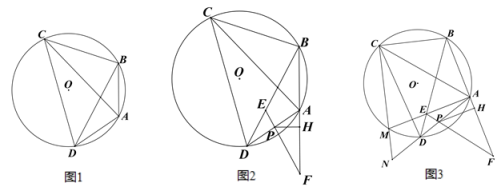
(1)如图 1,求证:点 A 为弧 BD 的中点;
(2)如图 2,点 E 为弦 BD 上一点,延长 BA 至点 F,使得 AF=AB,连接 FE 交 AD 于点 P,过点 P 作 PH⊥AF 于点 H,AF=2AH+AP,求证:AH:AB=PE:BE;
(3)在(2)的条件下,如图 3,连接 AE,并延长 AE 交⊙O 于点 M,连接 CM,并延长 CM 交 AD 的延长线于点 N,连接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的长.
,求 AH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
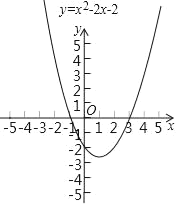
【题目】在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com