
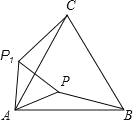
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线W:y=ax2﹣2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).
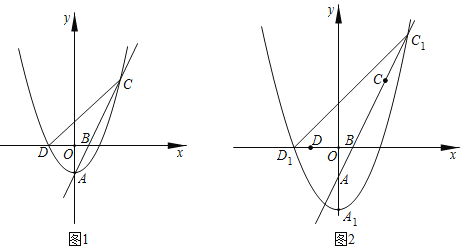
(1)求直线AB的解析式;
(2)过点C作CE⊥x轴,交x轴于点E,若AC平分∠DCE,求抛物线W的解析式;
(3)若a=![]() ,将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.
,将抛物线W向下平移m(m>0)个单位得到抛物线W1,如图2,记抛物线W1的顶点为A1,与x轴负半轴的交点为D1,与射线BC的交点为C1.问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B点,与y轴交于点C(0,﹣3).
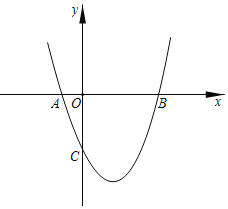
(1)求该抛物线的解析式;
(2)观察图象,直接写出不等式x2+bx+c>0的解集;
(3)设(1)中的抛物线上有一个动点P,点P在该抛物线上滑动且满足S△PAB=8,请求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+1=0中,b=![]() ;
;
(1)若a=4,求b的值;
(2)若方程ax2+bx+1=0有两个相等的实数根,求方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
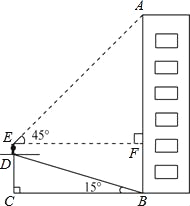
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,台风中心位于点![]() ,并沿东北方向
,并沿东北方向![]() 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,![]() 市位于点
市位于点![]() 的北偏东75°方向上,距离
的北偏东75°方向上,距离![]() 点480千米.
点480千米.

(1)说明本次台风是否会影响![]() 市;
市;
(2)若这次台风会影响![]() 市,求
市,求![]() 市受台风影响的时间.
市受台风影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌的洗衣机在市场上享有美誉,市场标价为![]() 元,进价为
元,进价为![]() 元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为
元,市场调研发现,若在市场价格的基础上降价会引起销售量的增加,当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台;当销售价格为
台;当销售价格为![]() 元时,月销售量为
元时,月销售量为![]() 台.若月销售量
台.若月销售量![]() (台)与销售价格
(台)与销售价格![]() (元)满足一次函数关系.
(元)满足一次函数关系.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)公司决定采取降价促销,迅速占领市场的方案,请根据以上信息,判断当销售价格![]() 定为多少元时,公司的月利润
定为多少元时,公司的月利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com