
【题目】在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)通过观察、测量、猜想: ![]() =
= ![]() ,并结合图②证明你的猜想;
,并结合图②证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求 ![]() 的值.(用含α的式子表示)
的值.(用含α的式子表示)
【答案】
(1)
证明:∵四边形ABCD是正方形,P与C重合,
∴OB=OP,∠BOC=∠BOG=90°,
∵PF⊥BG,∠PFB=90°,
∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,
∴∠GBO=∠EPO,
在△BOG和△POE中, 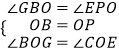 ,
,
∴△BOG≌△POE(ASA)
(2)
解:猜想 ![]() =
= ![]() .
.
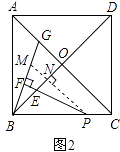
证明:如图2,过P作PM∥AC交BG于M,交BO于N,
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中, 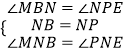 ,
,
∴△BMN≌△PEN(ASA),
∴BM=PE.
∵∠BPE= ![]() ∠ACB,∠BPN=∠ACB,
∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中,  ,
,
∴△BPF≌△MPF(ASA).
∴BF=MF.
即BF= ![]() BM.
BM.
∴BF= ![]() PE.
PE.
即 ![]() ;
;
(3)
解:如图3,过P作PM∥AC交BG于点M,交BO于点N,
∴∠BPN=∠ACB=α,∠PNE=∠BOC=90°.
由(2)同理可得BF= ![]() BM,∠MBN=∠EPN,
BM,∠MBN=∠EPN,
∴△BMN∽△PEN,
∴ ![]() .
.
在Rt△BNP中,tanα= ![]() ,
,
∴ ![]() =tanα.即
=tanα.即 ![]() =tanα.
=tanα.
∴ ![]() tanα.
tanα.

【解析】(1)由四边形ABCD是正方形,P与C重合,易证得OB=OP,∠BOC=∠BOG=90°,由同角的余角相等,证得∠GBO=∠EPO,则可利用ASA证得:△BOG≌△POE;(2)首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF= ![]() BM.则可求得
BM.则可求得 ![]() 的值;(3)首先过P作PM∥AC交BG于点M,交BO于点N,由(2)同理可得:BF=
的值;(3)首先过P作PM∥AC交BG于点M,交BO于点N,由(2)同理可得:BF= ![]() BM,∠MBN=∠EPN,继而可证得:△BMN∽△PEN,然后由相似三角形的对应边成比例,求得
BM,∠MBN=∠EPN,继而可证得:△BMN∽△PEN,然后由相似三角形的对应边成比例,求得 ![]() .
.


科目:初中数学 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).
根据以上统计图提供的信息,请解答下列问题:
(1)m= , n= .
(2)补全上图中的条形统计图.
(3)若全校共有2000名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线y= ![]() x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元. 
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线. 
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为2,E为AB边的中点,点F是BC边上一个动点,把△BEF沿EF向形内部折叠,点B的对应点为B′,当B′D的长最小时,BF长为( ) 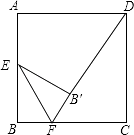
A.![]()
B.![]() ﹣1
﹣1
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F. 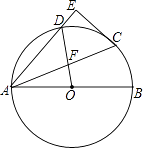
(1)求证:∠BAC=∠DAC;
(2)若AF:FC=6:5,求sin∠BAC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
A.8
B.10
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com