
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
【答案】
(1)解:由题意可知,抛物线的对称轴为直线x=6,
∴设抛物线的解析式为y=a (x-6)2+k,
∵抛物线经过点A(3,0)和C(0,9),
∴将A,C两点坐标代入得: ![]() ,解得:a=
,解得:a= ![]() ,k=-3.
,k=-3.
∴抛物线的解析式为y= ![]() (x-6)2-3
(x-6)2-3
(2)解:连接AE,
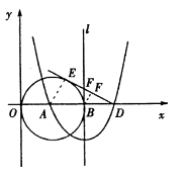
∵DE是⊙A的切线,
∴∠AED=90°,AE=3 ,
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,
∴AB=BD=3,
∴AD=6 , 在Rt△ADE中,DE2=AD2-AE2=62-32=27,
∴DE=3 ![]()
(3)解:利用有两个角对应相等的两个三角形相似,
当BF⊥ED时,∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,∴ ![]() ,即
,即 ![]() ,
,
∴BF= ![]() .
.
当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD ,
∴ ![]() 即BF=
即BF= ![]()
![]() ,
,
∴当△BFD与△EAD相似时,BF的长为 ![]() 或
或 ![]() .
.
【解析】(1)根据题意可知此抛物线的对称轴为x=6,设抛物线的解析式为顶点式,再将点A、C两点坐标代入解析式,建立方程求解,即可求出此函数解析式。
(2) 由DE是⊙A的切线,因此添加辅助线连接AE,得出∠AED=90°,AE=3 ,再根据圆的对称性及抛物线的对称性,求出AD的长, 在Rt△ADE中,利用勾股定理求出DE的长。
(3)抓住已知点F是切线DE上的一个动点,要使△BFD与△EAD相似,图形中隐含公共角∠ADE=∠BDF,因此分两种情况:当BF⊥ED时;当FB⊥AD时,根据相似三角形的性质,得出对应边成比例,建立方程,即可求出BF的长。


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
A.π
B.![]()
![]() π
π
C.![]() π
π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给的信息解答下列问题:
(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.

(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)SADC:SADB .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°,求这个角的度数;
(2)如图,点 C、D在线段 AB上, D是线段 AB的中点, AC ![]() AD , AB6,求线段 CD的长.
AD , AB6,求线段 CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三条边的长度分别是![]() ,
,![]() ,
,![]() ,记△ABC的周长为C△ABC.
,记△ABC的周长为C△ABC.
(1)当x=2时,△ABC的最长边的长度是 (请直接写出答案);
(2)请求出C△ABC(用含x的代数式表示,结果要求化简);
(3)我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=![]() .其中三角形边长分别为a,b,c,三角形的面积为S.
.其中三角形边长分别为a,b,c,三角形的面积为S.
若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com