[题目]如图.在△ABC中.∠C=90°.AC=6.BC=8．(1)用直尺和圆规作∠A的平分线.交BC于点D,(要求:不写作法.保留作图痕迹)(2)SADC:SADB ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在△ABC中，∠C=90°，AC=6，BC=8．

（1）用直尺和圆规作∠A的平分线，交BC于点D；（要求：不写作法，保留作图痕迹）

（2）SADC：SADB ．（直接写出结果）

【答案】（1）答案见解析；（2）

【解析】

（1）利用基本作图（作已知角的角平分线）作AD；

（2）过D作DE⊥AB于E．由角平分线的性质得到CD=DE．

在△ABC中，根据勾股定理求出AB的长，然后利用三角形面积公式计算即可得出结论．

（1）如图：

AD就是所求的射线；

（2）过D作DE⊥AB于E．

∵AD是角平分线，∠C=90°，∴CD=DE．

在△ABC中，∵∠C=90°，AC=6，BC=8，∴AB===10．

SADC：SADB=ACCD：（ABDE）=AC：AB=6：10=．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，已知A为⊙O外一点，连结OA交⊙O于P，AB为⊙O的切线，B为切点，AP＝5㎝，AB＝㎝，则劣弧与AB，AP所围成的阴影的面积是.

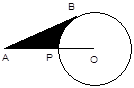
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】探究：

如图①，在△ABC中，点D、E、F分别在边AB、AC、CB上，且DE∥BC，EF∥AB，若∠ABC＝65°，求∠DEF的度数．请将下面的解答过程补充完整，并填空(理由或数学式)：

解：∵DE∥BC(　　)

∴∠DEF＝　　(　　)

∵EF∥AB

∴　　＝∠ABC(　　)

∴∠DEF＝∠ABC(　　)

∵∠ABC＝65°

∴∠DEF＝　　

应用：

如图②，在△ABC中，点D、E、F分别在边AB、AC、BC的延长线上，且DE∥BC，EF∥AB，若∠ABC＝β，则∠DEF的大小为　　(用含β的代数式表示)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某巡警车在一条南北大道上巡逻，某天巡警车从岗亭处出发，规定向北方向为正，当天行驶纪录如下（单位：千米）

﹣10，﹣9，+7，﹣15，+6，﹣5，+4，﹣2

（1）最终巡警车是否回到岗亭处？若没有，在岗亭何方，距岗亭多远？

（2）摩托车行驶1千米耗油0.2升，油箱有油10升，够不够？若不够，途中还需补充多少升油？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．

（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长．