
【题目】探究:
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):

解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
【答案】探究:见解析;应用:见解析.
【解析】
探究:依据两直线平行,内错角相等以及两直线平行,同位角相等,即可得到∠DEF=∠ABC,进而得出∠DEF的度数.应用:依据两直线平行,同位角相等以及两直线平行,同旁内角互补,即可得到∠DEF的度数.
解:探究:∵DE∥BC(已知)
∴∠DEF=∠CFE(两直线平行,内错角相等)
∵EF∥AB
∴∠CFE=∠ABC(两直线平行,同位角相等)
∴∠DEF=∠ABC(等量代换)
∵∠ABC=65°
∴∠DEF=65°
故答案为:已知;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等;等量代换;65°.
应用:∵DE∥BC
∴∠ABC=∠D=β
∵EF∥AB
∴∠D+∠DEF=180°
∴∠DEF=180°﹣∠D=180°﹣β,
故答案为:180°﹣β.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作角的平分线”的尺规作图的过程.
已知:如图1,![]() .
.
求作:射线![]() ,使它平分
,使它平分![]() .
.
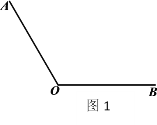
作法:如图2,
①以点![]() 为圆心,任意长为半径作弧,交
为圆心,任意长为半径作弧,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
②分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的同样长为半径作弧,两弧交于点
的同样长为半径作弧,两弧交于点![]() ;
;
③作射线![]() .
.
所以射线![]() 就是所求作的射线.
就是所求作的射线.
根据小明设计的尺规作图的过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
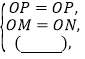
∴![]() ≌
≌![]() ( )(填推理的依据).
( )(填推理的依据).
∴ (全等三角形的 相等).
即射线![]() 平分
平分![]() (角平分线定义).
(角平分线定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下面的问题:
(1)如果a2+a=3,求a2+a+2015的值.
(2)已知a﹣b=﹣3,求3(b﹣a)2﹣5a+5b+5的值.
(3)已知a2+2ab=﹣3,ab﹣b2=﹣5,求4a2+![]() ab+
ab+![]() b2的值.
b2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给的信息解答下列问题:
(1)这次评价中,一共抽查了名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.

(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)SADC:SADB .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值.
①(x﹣1)(x+1)=x2﹣1
②(x﹣1)(x2+x+1)=x3﹣1
③(x﹣1)(x3+x2+x+1)=x4﹣1
……
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)=
请你利用上面的结论,再完成下面两题的计算:
(1)(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1
(2)若x3+x2+x+1=0,求x2019的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com