
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

【答案】(1)A(4,0),B(0,8);(2)S =﹣4m+16,(0<m<4);(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)根据坐标轴上点的特点直接求值,
(2)①由点在直线AB上,找出m与n的关系,再用三角形的面积公式求解即可;
②判断出EF最小时,点P的位置,根据三角形的面积公式直接求解即可.
试题解析:
(1)令x=0,则y=8,
∴B(0,8),
令y=0,则﹣2x+8=0,
∴x=4,
∴A(4,0),
(2)∵点P(m,n)为线段AB上的一个动点,
∴﹣2m+8=n,∵A(4,0),
∴OA=4,
∴0<m<4
∴S△PAO=![]() OA×PE=
OA×PE=![]() ×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4);
×4×n=2(﹣2m+8)=﹣4m+16,(0<m<4);
(3)存在,理由如下:
∵PE⊥x轴于点E,PF⊥y轴于点F,OA⊥OB,
∴四边形OEPF是矩形,
∴EF=OP,
当OP⊥AB时,此时EF最小,
∵A(4,0),B(0,8),
∴AB=4![]() ,
,
∵S△AOB=![]() OA×OB=
OA×OB=![]() AB×OP,
AB×OP,
∴OP=![]() ,
,
∴EF最小=OP=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
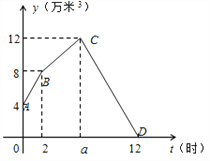
【题目】某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.
若这3个水口的水流都是匀速的,且2个进水口的水流速度一样,水池中的蓄水量 y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:
(1)蓄水池中原有蓄水 万米3,蓄水池达最大蓄水量12万米3的时间a的值为 ;
(2)求线段BC、CD所表示的y与t之间的函数关系式;
(3)蓄水池中蓄水量维持在m万米3以上(含m万米3)的时间有3小时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0)
B.(3,0)
C.(a,0)
D.(-b,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①两负数比较大小,绝对值大的反而小;
②数轴上,在原点左边离原点越近的数越小;
③所有的有理数都可以用数轴上的点表示;
④倒数等于它本身的数是1或0;
⑤两数相加,和一定大于任何一个加数.
其中正确的有( )
A.①④
B.②③④
C.①③
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中是平面图形的个数为( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com