
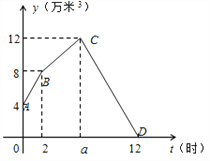
����Ŀ��ijˮ��վ�˽���һ�������ˮ����Ϊ12����3����ˮ�أ�������2��������ͬ�Ľ�ˮ�ں�1����ˮ�ڣ�ij���0ʱ��12ʱ�����л���������.���У�0ʱ��2ʱ��2����ˮ�ڽ�ˮ��2ʱ���ر�1����ˮ�ڼ�����ˮ�ٶȣ�����ˮ����ˮ���ﵽ�����ˮ�������漴�ر���һ����ˮ�ڣ�����ˮ�ڣ�ֱ��12ʱ��ˮ���е�ˮ����Ϊֹ.
����3��ˮ�ڵ�ˮ���������ٵģ���2����ˮ�ڵ�ˮ���ٶ�һ����ˮ���е���ˮ�� y������3����ʱ��t��ʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����������⣺
��1����ˮ����ԭ����ˮ ����3����ˮ�ش������ˮ��12����3��ʱ��a��ֵΪ ��
��2�����߶�BC��CD����ʾ��y��t֮��ĺ�����ϵʽ��
��3����ˮ������ˮ��ά����m����3���ϣ���m����3����ʱ����3Сʱ����m��ֵ��
���𰸡���1��4��6����2��yBC=x+6����2��x��6����![]() .��6��x��12��;(3)10
.��6��x��12��;(3)10
�������������������1�����ݺ���ͼ����Եõ���ˮ����ԭ����ˮ���������2��������ͬ�Ľ�ˮ�ں�ͼ��������a��ֵ��
��2�����ݺ���ͼ����Էֱ�����߶�BC��CD����ʾ��y��t֮��ĺ�����ϵʽ��
��3���������֪��BC�ϵĺ���ֵ��CD�ϵĺ���ֵ��ȣ��ҷֱ��Ӧ��ʱ���ֵΪ3���Ӷ��������m��ֵ��
�⣺(1)��ͼ���֪,��ˮ����ԭ����ˮ4����3,
��ˮ�ش������ˮ��12����3��ʱ��a��ֵΪ��2+(128)��(842��12)=6��
�ʴ�Ϊ��4��6��
(2)��B(2,8),C(6,12),��ֱ��BC�ĺ�����ϵʽΪy=k1x+b1��
������,��![]() ��
��
��ã� ![]() .
.
��ֱ��BC����Ӧ�ĺ�����ϵʽΪy=x+6(2x6)��
��C(6,12),D(12,0),��ֱ��CD�ĺ�����ϵʽΪy=k2x+b2��
������,��![]() ��
��
��ã� ![]() .
.
��ֱ��CD����Ӧ�ĺ�����ϵʽΪy=2x+24(6x12)��
(3)����BC����ˮ���ﵽm����3��ʱ��Ϊt,����CD����ˮ���ﵽm����3��ʱ��Ϊ(t+3)h��
������,��t+6=2(t+3)+24��
��ã�t=4��
�൱ t=4ʱ��y=4+6=10
��m��ֵ��10.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С���A�س������ڶ���·�ϼ�����·�����涨����ʻ��·��Ϊ������������ʻ��·��Ϊ������һ������ʻ��¼����λ��ǧ�ף����£� ![]()
��1���չ�ʱ����С����A�ص��IJ࣬��A�ض�Զ��
��2����ÿǧ����0.3�����ӳ������չ������Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��������,�̼�����ij�ֽ���Ϊ600Ԫ�����Ϊ1200Ԫ����Ʒ���д�������,��Ҫ��֤�����ʲ�����10%,������ۿ���( )
A.5��
B.5.5��
C.6��
D.6.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
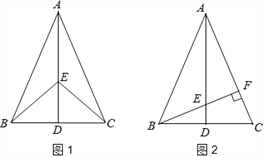
����Ŀ����ͼ1������ABC�У�AB=AC����D��BC���е㣬��E��AD�ϣ�
��1����֤��BE=CE��
��2����ͼ2����BE���ӳ��߽�AC�ڵ�F����BF��AC������ΪF����BAC=45����ԭ���������������䣮��֤����AEF�ա�BCF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��25��ͬѧ�μ�ij�������Ԥ���ɼ�������ͬ��ȡǰ13���μӾ���������һ��ͬѧ�Ѿ�֪���Լ��ijɼ����ܷ���������ֻ��Ҫ��֪����25��ͬѧ�ɼ���( )
A.��߷�
B.���
C.����
D.ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ֱ֪��AB�ĺ�������ʽΪy=��2x+8����x�ύ�ڵ�A����y�ύ�ڵ�B��
��1����A��B��������ꣻ
��2������P��m��n��Ϊ�߶�AB�ϵ�һ�����㣨��A��B���غϣ�����PE��x���ڵ�E��PF��y���ڵ�F������EF���ʣ�
������PAO�����ΪS����S����m�ĺ�����ϵʽ����д��m��ȡֵ��Χ��
���Ƿ���ڵ�P��ʹEF��ֵ��С�������ڣ����EF����Сֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com