
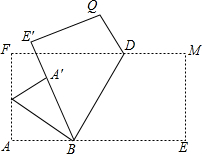
 将一张长方形纸片的一角折叠,使点A落在A′处,BC为折痕,然后把BE折过去,使之与A′B重合,折痕为BD,那么两条折痕BC与BD的夹角是多少度?
将一张长方形纸片的一角折叠,使点A落在A′处,BC为折痕,然后把BE折过去,使之与A′B重合,折痕为BD,那么两条折痕BC与BD的夹角是多少度?  一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
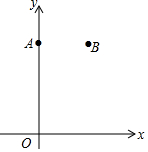 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
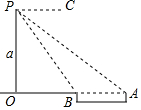 如图所示,直升机在长江大桥AB上方P点处,此时飞机离地面高度为akm,且A,B,O三点在一条直线上,测得点A的俯角为α,点B的俯角为β,求长江大桥AB的长度.
如图所示,直升机在长江大桥AB上方P点处,此时飞机离地面高度为akm,且A,B,O三点在一条直线上,测得点A的俯角为α,点B的俯角为β,求长江大桥AB的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
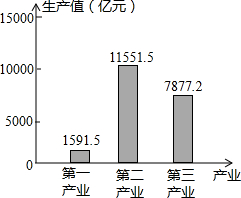 如图是2002年第一季度国内生产总值(亿元)统计图
如图是2002年第一季度国内生产总值(亿元)统计图查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com