练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

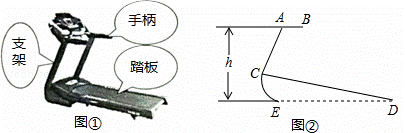
    图①、②分别是某种型号跑步机的实物图与示意图，已知踏板CD长为1．6m，CD与地面DE的夹角∠CDE为12°，支架AC长为0．8m，∠ACD为80°，求跑步机手柄的一端A的高度h（精确到0．1m）．

    （参考数据：sin12°=cos78°≈0．21，sin68°=cos22°≈0．93，tan68°≈2．48）


    解：过C点作FG⊥AB于F，交DE于G．

    ∵CD与地面DE的夹角∠CDE为12°，∠ACD为80°，

    ∴∠ACF=90°+12°﹣80°=22°，

    ∴∠CAF=68°，

    在Rt△ACF中，CF=AC•sin∠CAF≈0.744m，

    在Rt△CDG中，CG=CD•sin∠CDE≈0.336m，

    ∴FG=FC+CG≈1.1m．

    故跑步机手柄的一端A的高度约为1.1m．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知抛物线y=ax2+x+c（a≠0）经过A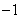（，0），B（2，0）两点，与y轴相交于点C．

    （1）求该抛物线的解析式；

    （2）点E是该抛物线上一动点，且位于第一象限，当点E到直线BC的距离最大时，求点E的坐标；

    （3）在（2）的条件下，在x轴上有一点P，且∠EAO+∠EPO=∠α，当tanα=2时，求点P的坐标．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用配方法解方程：2x2－4x－1＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


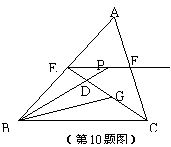
    如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于点D，∠CBP的平分线交CE于G，当CG=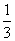CE时， EP+BP=______．

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


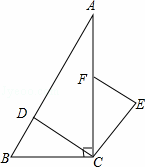
    如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

    （1）求证：△BCD≌△FCE；

    （2）若EF∥CD，求∠BDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列几何体中，同一个几何体的主视图与俯视图不同的是（　　）

    　

    A.             B.               C.               D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果分式的值为零，那么x＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明同学在“百度”搜索引擎中输入“中国梦，我的梦”，能搜索到与之相关的结果的条数是，这个数用科学记数法表示为

           A．      B．      C．   D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，将一副三角板叠放在一起，使直角的顶点重合于点O，则∠AOC+∠DOB的度数为
    __________．

    查看答案和解析>>

    同步练习册答案