
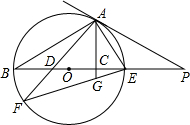
 (2013•竹溪县模拟)如图BE是⊙O的直径,点A是⊙O上一点,连结AE,延长BE至点P,连结PA,∠PAE=∠ABE,过点A作AC⊥BE于点C,点D是BO上一点,直线AD交⊙O于点F,连结FE与直线AC交于点G.
(2013•竹溪县模拟)如图BE是⊙O的直径,点A是⊙O上一点,连结AE,延长BE至点P,连结PA,∠PAE=∠ABE,过点A作AC⊥BE于点C,点D是BO上一点,直线AD交⊙O于点F,连结FE与直线AC交于点G.| 1 | 2 |
| AE |
| EG |
| EF |
| AE |

| 1 |
| 2 |
| CE |
| AC |
| AC |
| BC |
| CE |
| AC |
| 12 |
| 5 |
| 12 |
| 5 |
| AE |
| EG |
| EF |
| AE |


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
(2013•竹溪县模拟)某班50名学生的一次英语听力测试成绩分布如表所示(满分10分):
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断:
(2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断:查看答案和解析>>
科目:初中数学 来源: 题型:
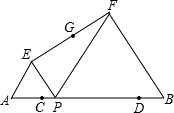 (2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是
(2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是查看答案和解析>>
科目:初中数学 来源: 题型:
| 竹溪土特产种类 | A | B | C |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨土特产获利(百元) | 12 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 1 |
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com