解:(1)∵△=(2k+1)
2-4×4(k-

)
=4k
2+4k+1-16k+8
=4k
2-12k+9
=(2k-3)
2,
∵(2k-3)
2,≥0,
∴△≥0,
∴无论k取什么实数,这个方程总有实数根;
(2)∵x=
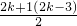
∴x
1=2,x
2=2k-1,
①当以2为腰,2k-1为底,则三角形的周长为2k+3;
当以2为底,2k-1为腰时,三角形的周长为4k.
②当以2为腰,2k-1为底时,

<k<

;
当以2为底,2k-1为腰时,k>1.
分析:(1)先求出△,变形为△=(2k-3)
2,得到△≥0,根据△的意义即可得到结论;
(2)利用求根公式先求出方程的两根x
1=2,x
2=2k-1,然后分类推论:当以2为腰或当以2为底,分别求出三角形的周长,再利用三角形的三边关系分别得到k的取值范围.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0)的根的判别式△=b
2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了代数式的变形、一元二次方程的解法和分类讨论的思想的运用以及三角形三边的关系.

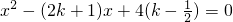 ,
, )
)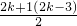
 <k<
<k< ;
;

 名校课堂系列答案
名校课堂系列答案