
【题目】如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE;过点F作FG⊥BC交BC的延长线于点G.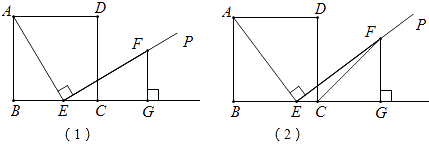
(1)求证:FG=BE;
(2)连接CF,如图(2),求证:CF平分∠DCG;
(3)当 ![]() =
= ![]() 时,求sin∠CFE的值.
时,求sin∠CFE的值.
【答案】
(1)
证明:∵EP⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
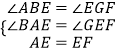 ,
,
∴△ABE≌△EGF(AAS),
∴FG=BE;
(2)
证明:由(1)知:BC=AB=EG,
∴BC﹣EC=EG﹣EC,
∴BE=CG,
又∵FG=BE,
∴FG=CG,
又∵∠CGF=90°,
∴∠FCG=45°= ![]() ∠DCG,
∠DCG,
∴CF平分∠DCG
(3)
解:如图,作CH⊥EF于H,
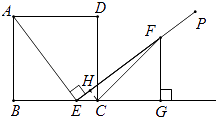
∵∠HEC=∠GEF,∠CHE=∠FGE=90°,
∴△EHC∽△EGF,
∴ ![]() =
= ![]() ,
,
根据 ![]() =
= ![]() ,设BE=3a,则EC=a,EG=4a,FG=CG=3a,
,设BE=3a,则EC=a,EG=4a,FG=CG=3a,
∴EF=5a,CF=3 ![]() a,
a,
∴ ![]() =
= ![]() ,HC=
,HC= ![]() a,
a,
∴sin∠CFE= ![]() =
= ![]() .
.
【解析】(1)根据同角的余角相等得到一对角相等,再由一对直角相等,且AE=EF,利用AAS得到三角形ABE与三角形EFG全等,利用全等三角形的对应边相等即可得证;(2)由(1)得到BC=AB=EG,利用等式的性质得到BE=CG,根据FG=BE,等量代价得到FG=CG,即三角形FCG为等腰直角三角形,得到∠FCG=45°,即可得证;(3)如图,作CH⊥EF于H,则△EHC∽△EGF,利用相似得比例,根据BE与BC的比值,设出BE,EC,以及EG,FG,利用勾股定理表示出EF,CF,进而表示出HC,在直角三角形HC中,利用锐角三角函数定义即可求出sin∠CFE的值.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,点O是△ABC的内心,连接OB、OC,过点O作EF∥BC分别交AB、AC于点E、F,已知BC=a (a是常数),设△ABC的周长为y,△AEF的周长为x,在下列图象中,大致表示y与x之间的函数关系的是( )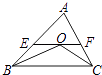
A.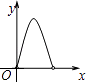
B.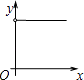
C.
D.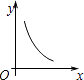
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
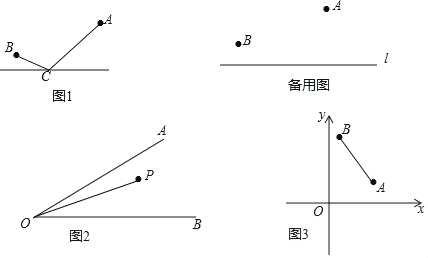
【题目】唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望峰火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题我们称之为“饮马问题”.如图1所示,诗中将军在观望烽火之后从山脚下的A点出发,走到河旁边的C点饮马后再到B点宿营.请问怎样走才能使总的路程最短?某课题组在探究这一问题时抽象出数学模型:
直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.
解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为线段A′B的长.
(1)根据上面的描述,在备用图中画出解决“饮马问题”的图形;
(2)利用轴对称作图解决“饮马问题”的依据是 .
(3)应用:①如图2,已知∠AOB=30°,其内部有一点P,OP=12,在∠AOB的两边分别有C、D两点(不同于点O),使△PCD的周长最小,请画出草图,并求出△PCD周长的最小值;
②如图3,点A(4,2),点B(1,6)在第一象限,在x轴、y轴上是否存在点D、点C,使得四边形ABCD的周长最小?若存在,请画出草图,并求其最小周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) 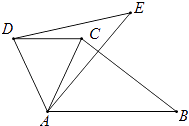
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE;过点F作FG⊥BC交BC的延长线于点G.
(1)求证:FG=BE;
(2)连接CF,如图(2),求证:CF平分∠DCG;
(3)当 ![]() =
= ![]() 时,求sin∠CFE的值.
时,求sin∠CFE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A的坐标为(2,0),点P在直线y=x上运动,当以点P为圆心,PA的长为半径的圆的面积最小时,点P的坐标为( )
A.(1,﹣1)
B.(0,0)
C.(1,1)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
A.600﹣250 ![]() 米
米
B.600 ![]() ﹣250米
﹣250米
C.350+350 ![]() 米
米
D.500 ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( ) 
A.80°
B.100°
C.60°
D.45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com