(1)证明:∵四边形BDEC内接于⊙O
∴∠AED=∠ABC
又∵∠A=∠A,
∴△ADE∽△ACB
(2)解:作CF⊥AB的延长线于F
已知∠ABC=120°,∠CBF=60°

在直角△BCF中,BF=BC•cos60°=
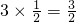
,
CF=BC•sin60°=

∴AF=AB+BF=

在直角△ACF中,

,
由△ADE∽△ACB知

,即

∴

(0<x<5)
(3)解:设方程x
2-mx+9=0的两根为x
1和x
2且x
1和x
2是正整数,则x
1•x
1=9
∴x
1=9,x
2=1或x
1=x
2=3
又∵AD<AB,AB=5∴AD=1或AD=3
①当AD=1时,m=x
1+x
2=10
∵△ABC∽△AED∴

∴

,

作DG⊥AC于G
∵四边形BCED内接于⊙O
∴∠DEG=180°-∠CBD=180°-120°=60°
∴在Rt△DEG中DG=DE•sin60°=

∴S
四边形BCED=S
△ABC-S
△AED=

=

=

②当AD=3时,m=x
1+x
2=6,
与①同理,得

∴S
四边形BCED=S
△ABC-S
△AED=

=

分析:(1)因为四边形BDEC内接于⊙O,所以∠AED=∠ABC,再根据已知条件可证明△ADE∽△ACB.
(2)设AD=x,CE=y,作CF⊥AB的延长线于F,因为△ADE∽△ACB,可用x,y表示出BF,CF,AF的长,根据相似三角形的对应边成比例,可求出函数式.
(3)设方程x
2-mx+9=0的两根为x
1和x
2且x
1和x
2是正整数,则x
1•x
1=9所以x
1=9,x
2=1或x
1=x
2=3又因为,AD<AB,AB=5所以AD=1或AD=3,因此根据这两种情况可求解.
点评:本题考查了圆内接四边形的性质,相似三角形的判定和性质定理,以及根与系数的关系,勾股定理等知识点.

 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,D是AB上一点,且D与A、B不重合,过 B、C、D三点的⊙O交AC于点E,连接DE
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,D是AB上一点,且D与A、B不重合,过 B、C、D三点的⊙O交AC于点E,连接DE
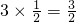 ,
,

 ,
, ,即
,即
 (0<x<5)
(0<x<5)
 ,
,









 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为