等腰梯形ABCD中,AD∥BC,∠B=45°,AD=4,BC=10,那么梯形ABCD的周长是________.
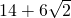
分析:过D作DE∥AB交BC于E,得到平行四边形ADEB,推出AD=BE=4,AB=DE,∠B=∠DEC=45°,求出CE的长和∠EDC=90°,设DE=DC=x,由勾股定理得:x
2+x
2=6
2,求出x的长,即可求出AB、CD的长,代入即可得到答案.
解答:
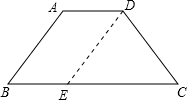
解:过D作DE∥AB交BC于E,
∵AD∥BC,DE∥AB,
∴四边形ADEB是平行四边形,
∴AD=BE=4,AB=DE,∠B=∠DEC=45°,
∴EC=10-4=6,
∵等腰梯形ABCD,
∴∠B=∠C=45°,
∴DE=DC,
∴∠EDC=180°-45°-45°=90°,
设DE=DC=x,由勾股定理得:x
2+x
2=6
2,
解得:x=3

,
∴AB=DC=3

,
∵AD=4,BC=10,
∴梯形ABCD的周长是AB+BC+DC+AD=14+6

,
故答案为:14+6

.
点评:本题考查了平行四边形的性质和判定,勾股定理,解一元二次方程,等腰梯形的性质,等腰三角形的判定等知识点,解此题的关键是把梯形转化成平行四边形和等腰三角形.

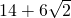
 解:过D作DE∥AB交BC于E,
解:过D作DE∥AB交BC于E, ,
, ,
, ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.