

分析 (1)首先证明DM=DN,再根据AAS即可判断.
(2)根据题意求出BO1、BO2、BO3,寻找规律后即可解决问题.
(3)结论:第二次折叠时,折痕一定会经过点A.作AE⊥BD垂足为E,求出BE的长,证明点E与点O2重合即可.
解答 (1)证明:如图①中,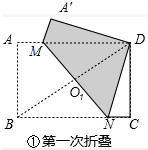
∵四边形MNDA′是由四边形MNBA翻折得到,
∴∠ABN=∠A′DN=90°,∠BNM=∠MND,
∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=90°,
∴∠BNM=∠DMN=∠DNM,
∴DM=DN,
∵∠A′DN=∠ADC,
∴∠A′DM=∠NDC,
在△DA′M和△DCN中,
$\left\{\begin{array}{l}{∠A′DM=∠NDC}\\{∠A′=∠C=90°}\\{DM=DN}\end{array}\right.$,
∴△DMA′≌△DNC.
(2)如图③中,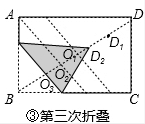 ,
,
∵四边形ABCD是矩形,
∴∠C=90°,AB=CD=$\sqrt{6}$,BC=AD=$\sqrt{10}$,
∴BD=$\sqrt{C{B}^{2}+C{D}^{2}}$=$\sqrt{16}$=4,
∵BO1=O1D=$\frac{1}{2}$BD=2=$\frac{{3}^{1-1}}{{2}^{2×1-3}}$,
BO2=$\frac{1}{2}$BD1=$\frac{3}{2}$=$\frac{{3}^{2-2}}{{2}^{2×2-3}}$,
BO3=$\frac{1}{2}$BD2=$\frac{9}{8}$=$\frac{{3}^{3-1}}{{2}^{2×3-3}}$,
…
BOn=$\frac{{3}^{n-1}}{{2}^{2n-3}}$.
(3)如图②中,结论:第二次折叠时,折痕一定会经过点A.
理由:作AE⊥BD垂足为E.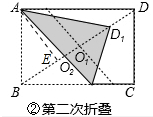
∵∠AEB=∠BAD=90°,∠ABE=∠BAD,
∴△ABE∽△DBA,
∴$\frac{BE}{BA}$=$\frac{BA}{BD}$,
∴$\frac{BE}{\sqrt{6}}$=$\frac{\sqrt{6}}{4}$,
∴BE=$\frac{3}{2}$,
∵BO2=$\frac{3}{2}$,
∴点E与点O2重合,
∴第二次折叠时,折痕一定会经过点A.
点评 本题考查四边形的综合题、矩形的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定和性质、翻折变换等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2a}$ | B. | -$\frac{1}{2a}$ | C. | -$\frac{1}{a}$ | D. | $\frac{1}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足为ID、E.
如图:已知在Rt△ABC中,∠ACB=90°,CD⊥AB,FE⊥AB,垂足为ID、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com