
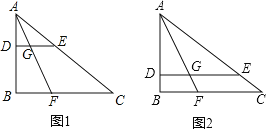
【题目】在Rt△ABC中,∠B=90°,点F在边BC上,tan∠FAC=![]() ,点E为斜边AC上一动点,ED⊥AB于点D,交AF于点G.
,点E为斜边AC上一动点,ED⊥AB于点D,交AF于点G.
(1)如图1,求证:![]() ;
;
(2)如图1,若AB=2DE,求证:![]() BF+AD=2GE;
BF+AD=2GE;
(3)如图2,若AB=DE=4,AD=3,直接写出FC的长 .
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由题意可得DE∥BC,可得△ADG∽△ABF,△AGE∽△AFC,由相似三角形性质可得![]() ,
,![]() ,可得结论;
,可得结论;
(2)在DB上截取DM=![]() BF,连接EM交AF于点N,通过证明△ABF∽△EDM,可得∠DME=∠AFB,∠BAF=∠DEM,可证∠ANE=90°,通过证明△AMN∽△EGN,可得
BF,连接EM交AF于点N,通过证明△ABF∽△EDM,可得∠DME=∠AFB,∠BAF=∠DEM,可证∠ANE=90°,通过证明△AMN∽△EGN,可得![]() ,由线段的和差关系,可得结论;
,由线段的和差关系,可得结论;
(3)过点F作FM⊥AC于点M,由勾股定理可求AE=5,由题意可证△ADE∽△ABC,可得![]() =
=![]() ,可求AC,BC的长,由锐角三角函数可求AM=2FM,MC=
,可求AC,BC的长,由锐角三角函数可求AM=2FM,MC=![]() FM,即可求FM的长,由勾股定理可求FC的长.
FM,即可求FM的长,由勾股定理可求FC的长.
(1)∵ED⊥AB,
∴∠ADE=90°,
∵∠B=90°,
∴∠B=∠ADE,
∴DE∥BC,
∴△ADG∽△ABF,△AGE∽△AFC
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
(2)如图,在DB上截取DM=![]() BF,连接EM交AF于点N,
BF,连接EM交AF于点N,
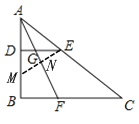
∵AB=2DE,DM=![]() BF,
BF,
∴![]() =
=![]() ,且∠ABF=∠EDM=90°
,且∠ABF=∠EDM=90°
∴△ABF∽△EDM
∴∠DME=∠AFB,∠BAF=∠DEM
∵∠BAF+∠AFB=90°
∴∠BAF+∠DME=90°
∴∠ANE=90°,
∵tan∠FAC=![]() =
=![]()
∵∠ANM=∠ANE,∠BAF=∠DEM
∴△AMN∽△EGN
∴![]()
∴AM=2GE,且AM=AD+DM=AD+![]() BF
BF
∴![]() BF+AD=2GE;
BF+AD=2GE;
(3)如图,过点F作FM⊥AC于点M,
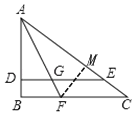
∵AD=3,DE=4,AD⊥DE
∴AE=5,
∵DE∥BC
∴△ADE∽△ABC
∴![]() =
=![]()
即![]() =
=![]()
∴AC=![]() ,BC=
,BC=![]()
∵tan∠FAC=![]() =
=![]()
∴AM=2FM,
∵tan∠C=![]()
∴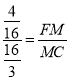
∴MC=![]() FM
FM
∵AM+MC=AC
∴2FM+![]() FM=
FM=![]()
∴FM=2,
∴MC=![]()
∴FC=![]() =
=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”,例如,方程
)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”,例如,方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则
是“倍根方程”,则![]() ______;
______;
(2)若![]() (
(![]() )是“倍根方程”,求代数式
)是“倍根方程”,求代数式![]() 的值;
的值;
(3)若方程![]() (
(![]() )是倍根方程,且相异两点
)是倍根方程,且相异两点![]() ,
,![]() ,都在抛物线
,都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() (
(![]() )的根.
)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
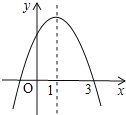
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论①abc>0②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3③4a+2b+c<0④当x>0时,y随x的增大而减小正确的是( ).
A.①③④B.②④C.①②③D.②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,BC平分∠ABD
(1) 若∠A=100°,则∠1的度数为_________
(2) 判断AC与BD的位置关系,并证明你的结论

查看答案和解析>>
科目:初中数学 来源: 题型:
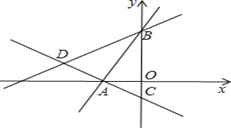
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A. 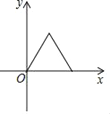 B.
B. 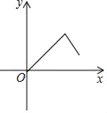 C.
C.  D.
D. 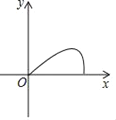
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,点D为BC上一点,连接AD.
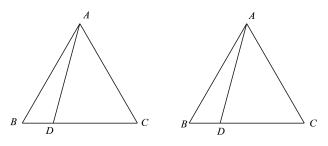
图1 图2
(1)若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;
(2)将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
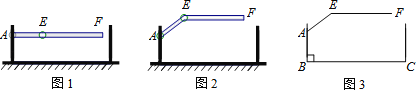
【题目】某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com