
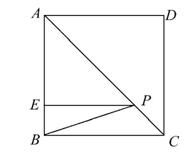
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
科目:初中数学 来源: 题型:
在△ABC中,BC=a,AC=b,AB=c,设c为最长边.当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边长分别为6,8,9时,△ABC为 三角形;当△ABC三边长分别为6,8,11时,△ABC为 三角形.
(2)猜想:当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
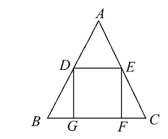
如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
A.3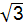 cm B.4cm
cm B.4cm
C.2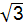 cm D.2
cm D.2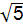 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停。已知一支股票某天涨停,之后两天时间又跌回到原价,若这两天此股票股价的平均每天下跌的百分率为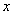 ,则
,则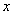 满足的方程是( )
满足的方程是( )
A.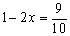 B.
B.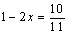 C.
C.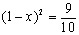 D.
D.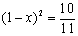
查看答案和解析>>
科目:初中数学 来源: 题型:
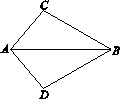
如图,△ABC沿AB向下翻折得到△ABD,若∠ABC=30°,
∠ADB=100°,则∠BAC的度数是( ).
A.30° B.100° C.50° D.80°
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com