

分析 (1)如图1中,连接AC.只要证明△DAF∽△CAM即可解决问题.
(2)如图2中,连接AC交BD于O.首先证明A、B、M、E四点共圆,再证明△AMC∽△AFD,由此求出DF、BF,再根据△KBF∽△KMA,得$\frac{BK}{KM}$=$\frac{BF}{AM}$=$\frac{\frac{6\sqrt{5}}{5}}{\sqrt{17}}$,设BK=$\frac{6\sqrt{5}}{5}$k,KM=$\sqrt{17}$k,在Rt△KBM中,利用勾股定理即可求出k,解决问题.
解答 (1)证明:如图1中,连接AC.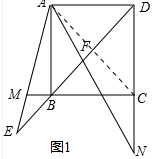
∵四边形ABCD是正方形,
∴∠ADB=∠ACM=∠DAC=45°,AC=$\sqrt{2}$AD,
∵∠MAN=∠BDA=45°,
∴∠MAN=∠DAC,
∴∠MAC=∠DAF,
∴△DAF∽△CAM,
∴$\frac{DF}{CM}$=$\frac{AD}{AC}$=$\frac{1}{\sqrt{2}}$,
∴CM=$\sqrt{2}$AD.
(2)如图2中,连接AC交BD于O.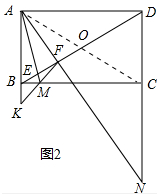
∵四边形ABCD是矩形,
∴OA=OD=OC=OB,∠ABC=∠KBM=90°,
∴∠OAD=∠ODA=∠OBC=∠OCB,
∵∠MAN=∠BDA,
∴∠MBE=∠MAF,
∴A、B、M、E四点共圆,
∴∠KBN=∠AFK=90°,
∵∠MAN=∠OAD,
∴∠MAC=∠FAD,∵∠ACM=∠ADF,
∴△AMC∽△AFD,
∴$\frac{DF}{CM}$=$\frac{AD}{AC}$,
∵AB=4,AD=8,tan∠BAM=$\frac{1}{4}$,
∴BM=1,AM=$\sqrt{17}$,AC=4$\sqrt{5}$,
∴$\frac{DF}{7}$=$\frac{8}{4\sqrt{5}}$,
∴DF=$\frac{14\sqrt{5}}{5}$,BF=BD-DF=$\frac{6\sqrt{5}}{5}$,
∵∠K=∠K,∠KAM=∠KFB,
∴△KBF∽△KMA,
∴$\frac{BK}{KM}$=$\frac{BF}{AM}$=$\frac{\frac{6\sqrt{5}}{5}}{\sqrt{17}}$,设BK=$\frac{6\sqrt{5}}{5}$k,KM=$\sqrt{17}$k,
在Rt△BKM中,∵BK2+MB2=KM2,
∴($\frac{6\sqrt{5}}{5}$k)2+1=($\sqrt{17}$k)2,
∵k>0,
∴k=$\frac{\sqrt{5}}{7}$,
∴BK=$\frac{6\sqrt{5}}{5}$×$\frac{\sqrt{5}}{7}$=$\frac{6}{7}$.
点评 本题考查四边形综合题、相似三角形的判定和性质.四点共圆等知识,解题的关键是灵活应用相似三角形的性质解决问题,四点共圆的发现是突破点,属于中考压轴题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,正方形ABCD中,连接对角线AC,将△ACD绕点C逆时针旋转一定角度得到△A′CD′,连接AA′,连接DD′并延长交AA′于点E,若A′E=$\frac{1}{2}$AC=2,则ED′=$\sqrt{6}$-$\sqrt{2}$.
如图所示,正方形ABCD中,连接对角线AC,将△ACD绕点C逆时针旋转一定角度得到△A′CD′,连接AA′,连接DD′并延长交AA′于点E,若A′E=$\frac{1}{2}$AC=2,则ED′=$\sqrt{6}$-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com