解:(1)∵直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),
∴
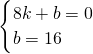
,
解得
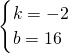
,
所以,直线AB的解析式为y=-2x+16,
联立
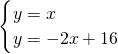
,
解得

,
所以,C点坐标为(

,

);
(2)根据题意,点D、E的纵坐标都是t,
所以,-2x+16=t,
解得x=

,
所以,点D(t,t),E(

,t),
DE=|

-t|,
∵点F在x轴上,
∴|

-t|=t,
即

-t=t或

-t=-t,
解得t=

或t=16,
所以,t的值为

,16;
(3)①PE∥AF时,点F在x轴上,根据(2)的结论,
t=

或16,
当t=16时,P、B、E三点重合,以A,E,P,F为顶点的是三角形,不符合题意舍去,
所以,t=

;
②PF∥AE时,点D在点E的左边,

∵D(t,t),E(

,t),
∴DE=

-t=
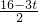
,
点F的纵坐标为:t-
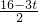
=
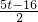
,
∴点F(t,
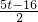
),
设直线PF的解析式为y=ex+f,
则
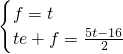
,
解得

,
所以,直线PF的解析式为y=
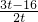
x+t,
∵PF∥AE,
∴
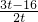
=-2,
解得t=

;
③AP∥EF时,(i)若点P在y轴正半轴,则DE=t-

=

,
点F的纵坐标为t-

=
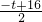
,
∴点F的坐标为(t,
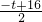
),
设直线EF的解析式为y=cx+d,则

,
解得
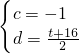
,
∴直线EF的解析式为y=-x+
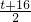
,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=-
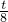
+t,
∵AP∥EF,
∴-
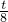
=-1,
解得t=8,

(ii)若点P在y轴负半轴,则DE=

-t=
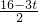
,
点F的纵坐标为t-
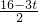
=
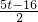
,
∴点F的坐标为(t,
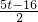
),
设直线EF的解析式为y=mx+n,则
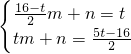
,
解得
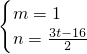
,
∴直线EF的解析式为y=x+

,
又∵A(8,0),P(0,t),
∴直线AP的解析式为y=-
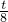
+t,
∵AP∥EF,
∴-
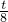
=1,
解得t=-8,
综上所述,t的值为

,

,8,-8.
分析:(1)把点A、B的坐标代入直线y=kx+b得到关于k、b二元一次方程组,求解得到k、b的值,即可得解,联立两直线解析式,求解即可得到点C的坐标;
(2)利用直线解析式表示出点D、E的坐标,然后求出DE的长度,再根据点F在x轴上,DE=DF列式计算即可得解;
(3)根据梯形的底边平行,分①PE∥AF时,点F在x轴上,根据(2)的结论解答,②PF∥AE时,先根据点D、E的坐标求出DE的长度,然后表示出点F的坐标,再利用待定系数法求出直线PF的解析式,然后根据平行直线的解析式的k值相等列式求解即可得到t的值;③AP∥EF时,分点P在y轴正半轴与负半轴两种情况求出DE的长度,然后表示出点F的坐标,再利用待定系数法求出直线AP、EF的解析式,然后根据平行直线的解析式的k值相等列式求解即可得到t的值.
点评:本题是一次函数的综合题型,主要涉及到待定系数法求一次函数解析式,联立两直线解析式求交点坐标,等腰直角三角形的性质,以及梯形的两底边互相平行,(3)求解思路比较复杂,且运算量较大,要分情况讨论求解.

 已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.
已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.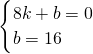 ,
,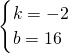 ,
,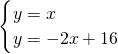 ,
, ,
, ,
, );
); ,
, ,t),
,t), -t|,
-t|, -t|=t,
-t|=t, -t=t或
-t=t或 -t=-t,
-t=-t, 或t=16,
或t=16, ,16;
,16; 或16,
或16, ;
;
 ,t),
,t), -t=
-t=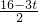 ,
,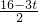 =
=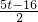 ,
,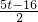 ),
),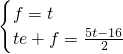 ,
, ,
,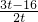 x+t,
x+t,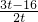 =-2,
=-2, ;
; =
= ,
, =
=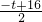 ,
,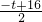 ),
), ,
,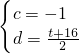 ,
,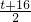 ,
,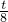 +t,
+t,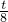 =-1,
=-1,
 -t=
-t=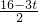 ,
,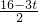 =
=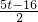 ,
,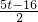 ),
),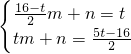 ,
,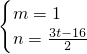 ,
, ,
,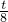 +t,
+t,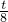 =1,
=1, ,
, ,8,-8.
,8,-8.

 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=