
某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个. 市场调查反映:如调整价格,每涨价1元,每天要少卖出10个;每降价1元,每天可多卖出30个。
(1)如果专卖店每天要想获得770元的利润,且要尽可能的让利给顾客,那么售价应涨价多少元?
(2)请你帮专卖店老板算一算,如何定价才能使利润最大,并求出此时的最大利润?
解:(1)设售价应涨价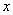 元,则:
元,则:
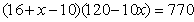 , …………………………………………2分
, …………………………………………2分
解得: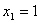 ,
,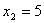 . ……………………………………………………3分
. ……………………………………………………3分
又要尽可能的让利给顾客,则涨价应最少,所以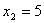 (舍去).
(舍去).
∴ 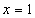 .
.
答:专卖店涨价1元时,每天可以获利770元. ……………………………4分
(2)设单价涨价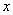 元时,每天的利润为
元时,每天的利润为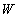 1元,则:
1元,则:
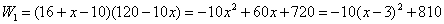 (0≤
(0≤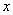 ≤12)
≤12)
即定价为:16+3=19(元)时,专卖店可以获得最大利润810元. ……6分
设单价降价z元时,每天的利润为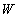 2元,则:
2元,则:
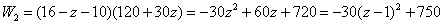 (0≤z≤6)
(0≤z≤6)
即定价为:16-1=15(元)时,专卖店可以获得最大利润750元. ………8分
综上所述:专卖店将单价定为每个19元时,可以获得最大利润810元. …10分


科目:初中数学 来源: 题型:
下面的表格列出了一个实验的统计数据,
表示将皮球从高处落下时,弹跳高度b与下降高度d的关系,
下面能表示这种关系的式子是( )
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
(A) (B)
(B) (C)
(C)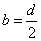 (D)
(D)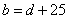
查看答案和解析>>
科目:初中数学 来源: 题型:
用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第n个图案中,所包含的黑色正三角形和白色正六边形的个数总和是( )。

A、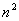 +4n+2 B、6n+1 C、
+4n+2 B、6n+1 C、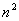 +3n+3 D、2n+4
+3n+3 D、2n+4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为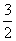 .其中,正确的结论是 。
.其中,正确的结论是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,……则第几个图形中圆和正三角形的个数相等.( ) .
 |
A. 7 B.8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
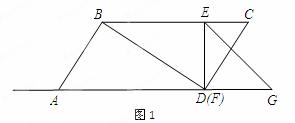
如图1,□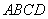 中,对角线
中,对角线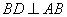 ,
,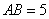 ,
, 边上
边上 的高为
的高为 .等腰直角
.等腰直角 中,
中, ,
, 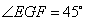 ,且
,且 与□
与□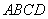 位于直线
位于直线 的同侧,点
的同侧,点 与点
与点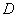 重合,
重合,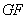 与
与 在同一直线上.
在同一直线上. 从点
从点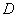 出发以每秒1个单位的速度沿射线
出发以每秒1个单位的速度沿射线 方向平移,当点
方向平移,当点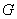 到点
到点 时停止运动;同时点
时停止运动;同时点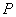 也从点
也从点 出发,以每秒3个单位的速度沿折线
出发,以每秒3个单位的速度沿折线 →
→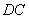 方向运动,到达点
方向运动,到达点 时停止运动,设运动的时间为
时停止运动,设运动的时间为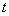 .
.
(1)求 的长度;
的长度;
(2)在 平移的过程中,记
平移的过程中,记 与
与 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 与运动时间
与运动时间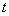 的函数关系式,并写出
的函数关系式,并写出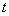 的取值范围;
的取值范围;
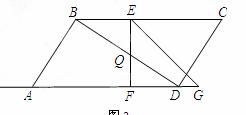
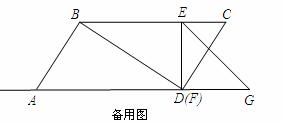
(3)如图2,在运动的过程中,若线段 与线段
与线段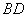 交于点
交于点 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间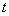 ,使得
,使得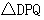 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的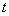 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
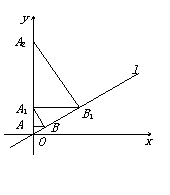
如图,已知直线l: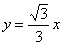 ,过点A(0,1)作y轴的垂线 交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为
,过点A(0,1)作y轴的垂线 交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点A4的坐标为
A.(0,64) B.(0,128) C.(0,256) D.(0,512)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com