练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，△ABC为等腰直角三角形，∠BAC=90°，BC=2，E为AB上任意一动点，以CE为斜边作等腰Rt△CDE，连接AD，下列说法：

    ①∠BCE=∠ACD；②AC⊥ED；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD的面积有最大值，且最大值为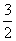．其中，正确的结论是            。



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    温度的变化，是人们常谈论的话题．下图是某地某天温度变化的情况．

    （1）上午8时的温度是多少？16时呢？

    （2）这一天的最高温度是多少？是在几时达到的？最低温度呢？

    （3）这一天的温差是多少？从最低温度到最高温度经过了多长时间？

    （4）在什么时间范围内温度在上升？在什么时间范围内温度在下降？

    （5）图中的A点表示的是什么？B点呢？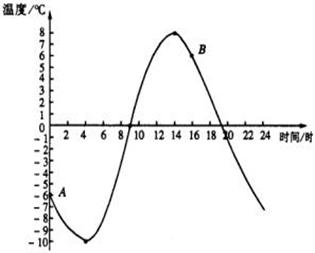


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等腰三角形的周长为12厘米，底边长为厘米，腰长为厘米. 则与的之间的关系式是        .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（　　）。

    A．　　B．　　C．　　D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知△ABC与△DEF相似且面积比为4︰9，则△ABC与△DEF的相似比为            。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     某梁平特产专卖店销售“梁平柚”，已知“梁平柚”的进价为每个10元，现在的售价是每个16元，每天可卖出120个. 市场调查反映：如调整价格，每涨价1元，每天要少卖出10个；每降价1元，每天可多卖出30个。

    （1）如果专卖店每天要想获得770元的利润，且要尽可能的让利给顾客，那么售价应涨价多少元？

    （2）请你帮专卖店老板算一算，如何定价才能使利润最大，并求出此时的最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，，平分，若， 则的度数是（     ）．

    A．100°             B．110°     C．120°             D．130°

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：，其中为不等式组

    的整数解.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在□ABCD中，已知AD＝5cm，AB＝3cm，AE平分∠BAD交BC边于点E，则EC等于

    A. 1.5cm        B. 2cm         

    C. 2.5cm        D. 3cm

    查看答案和解析>>

    同步练习册答案