
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкE.
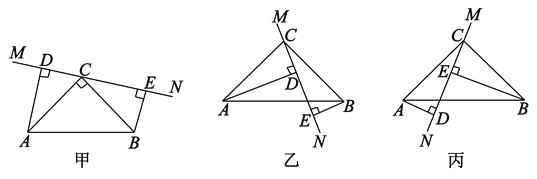
(1)ЕБжБЯпMNШЦЕуCа§зЊЕНЭММзЕФЮЛжУЪБЃЌЪдЫЕУїЃКЂйЁїADCЁеЁїCEBЃЛЂкDE=ADЃЋBEЃЛ
(2)ЕБжБЯпMNШЦЕуCа§зЊЕНЭМввЕФЮЛжУЪБЃЌЪдЫЕУїЃКDE=ADЃBEЃЛ
(3)ЕБжБЯпMNШЦЕуCа§зЊЕНЭМБћЕФЮЛжУЪБЃЌЪдЮЪDEЁЂADЁЂBEОпгадѕбљЕФЕШСПЙиЯЕЃПЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉADЁЂDEЁЂBEЫљТњзуЕФЕШСПЙиЯЕЪЧDE=BEЃAD(ЛђAD=BEЃDEЃЌBE=ADЃЋDEЕШ)РэгЩМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЁЯACB=90ЁуЃЌЕУЁЯBCEЃЋЁЯACD=90ЁуЃЌЖјADЁЭMNгкDЃЌBEЁЭMNгкE.дђЁЯADC=ЁЯCEB=90ЁуЃЌИљОнЕШНЧЕФгрНЧЯрЕШЕУЕНЁЯACD=ЁЯCBE.ЃЌвзЕУ
RtЁїADCЁеRtЁїCEBЃЌЫљвдAD=CEЃЌDC=BEЃЌМДПЩЕУЕНDE=DC+CE=BE+ADЃЎ
ЃЈ2ЃЉИљОнЕШНЧЕФгрНЧЯрЕШЕУЕНЁЯACD=ЁЯCBEЃЌвзЕУЁїADCЁеЁїCEB,ЕУЕНAD=CEЃЌDC=BEЃЌЫљвдDE=CE-CD=AD-BEЃЎ
ЃЈ3ЃЉDEЁЂADЁЂBEОпгаЕФЕШСПЙиЯЕЮЊЃКDE=BE-ADЃЎжЄУїЕФЗНЗЈгыЃЈ2ЃЉЯрЭЌЃЎ
ЪдЬтНтЮіЃК(1)ЂйЁпЁЯACB=90ЁуЃЌ
ЁрЁЯACD+ЁЯBCE=90ЁуЃЌ
ЖјADЁЭMNгкDЃЌBEЁЭMNгкEЃЌ
ЁрЁЯADC=ЁЯCEB=90ЁуЃЌЁЯBCE+ЁЯCBE=90ЁуЃЌ
ЁрЁЯACD=ЁЯCBE.
дкЁїADCКЭЁїCEBжа, 
ЁрЁїADCЁеЁїCEB(AAS)ЃЎ
ЂкЁпЁїADCЁеЁїCEBЃЌ
ЁрCE=ADЃЌCD=BEЃЌ
ЁрDE=CEЃЋCD=ADЃЋBEЃЛ
(2)ЁпЁЯADC=ЁЯCEB=ЁЯACB=90ЁуЃЌ
ЁрЁЯACD=ЁЯCBE.гжЁпAC=BCЃЌ
ЁрЁїADCЁеЁїCEB(AAS)ЃЌ
ЁрCD=BE.AD=CEЃЌ
ЁрDE=CEЃCD=ADЃBEЃЛ
(3)ЕБMNа§зЊЕНЭМБћЕФЮЛжУЪБЃЌADЁЂDEЁЂBEЫљТњзуЕФЕШСПЙиЯЕЪЧDE=BEЃAD(ЛђAD=BEЃDEЃЌBE=ADЃЋDEЕШ)ЃЎ
ЁпЁЯADC=ЁЯCEB=ЁЯACB=90ЁуЃЌ
ЁрЁЯACD=ЁЯCBE.
ЁпAC=BCЃЌ
ЁрЁїACDЁеЁїCBE(AAS)ЃЌ
ЁрAD=CEЃЌCD=BEЃЌ
ЁрDE=CDЃCE=BEЃAD.


 53ЬьЬьСЗЯЕСаД№АИ
53ЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїACBжаЃЌЁЯC=90ЁуЃЌBEЦНЗжЁЯABCЃЌEDДЙжБЦНЗжABгкDЃЎШєAC=9ЃЌЧѓAEЕФжЕЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌе§ЗНаЮABCOЕФЖЅЕуCЁЂAЗжБ№дкxЁЂyжсЩЯЃЌAЃЈ0ЃЌ6ЃЉЁЂEЃЈ0ЃЌ2ЃЉЃЌЕуHЁЂFЗжБ№дкБпABЁЂOCЩЯЃЌвдHЁЂEЁЂFЮЊЖЅЕузїСтаЮEFGH
ЃЈ1ЃЉЕБHЃЈЉ2ЃЌ6ЃЉЪБЃЌЧѓжЄЃКЫФБпаЮEFGHЮЊе§ЗНаЮ
ЃЈ2ЃЉШєFЃЈЉ5ЃЌ0ЃЉЃЌЧѓЕуGЕФзјБъ
ЃЈ3ЃЉШчЭМ2ЃЌЕуQЮЊЖдНЧЯпBOЩЯвЛЖЏЕуЃЌDЮЊБпOAЩЯвЛЕуЃЌDQЁЭCQЃЌЕуQДгЕуBГіЗЂЃЌбиBOЗНЯђвЦЖЏЃЎШєвЦЖЏЕФТЗОЖГЄЮЊ3ЃЌжБНгаДГіCDЕФжаЕуMвЦЖЏЕФТЗОЖГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y=2xЃ3ЕФЭМЯѓВЛОЙ§ЃЈ ЃЉ
A. ЕквЛЯѓЯо B. ЕкЖўЯѓЯо C. ЕкШ§ЯѓЯо D. ЕкЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЪЧЖлНЧЃЌЛГіЃК
(1)ЁЯBACЕФЦНЗжЯпЃЛ
(2)ACБпЩЯЕФжаЯпЃЛ
(3)ACБпЩЯЕФИпЃЛ
(4)ABБпЩЯЕФИпЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+3=0ЃЌЕБb=a+3ЪБЃЌЧыХаЖЯДЫЗНГЬИљЕФЧщПіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ5ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2ЃНpЕФвЛИіИљЃЌдђСэвЛИљЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіСНЮЛЪ§ЕФИіЮЛЪ§зжЮЊaЃЌЪЎЮЛЪ§зжБШИіЮЛЪ§зжЕФ2БЖЩй1ЃЌШєАбетИіСНЮЛЪ§ЪЎЮЛЩЯЕФЪ§зжгыИіЮЛЩЯЕФЪ§зжНЛЛЛЮЛжУзщГЩвЛИіаТСНЮЛЪ§ЃЌдђдСНЮЛЪ§гыаТСНЮЛЪ§ЕФВюЮЊЃЈ ЃЉ
A.9Љ9a
B.11aЉ11
C.9aЉ9
D.33aЉ11
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(БОЬтТњЗж8Зж)ШчЭМЃЌдкЁїABCжаЃЌCAЃНCBЃЌвдBCЮЊжБОЖЕФдВЁбOНЛACгкЕуGЃЌНЛABгкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌНЛCBЕФбгГЄЯпгкЕуEЃЌНЛACгкЕуF.

(1)ЧѓжЄЃКDFЁЭACЃЛ
(2)ШчЙћЁбOЕФАыОЖЮЊ5ЃЌABЃН12ЃЌЧѓcosE.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com