
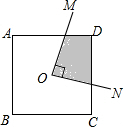
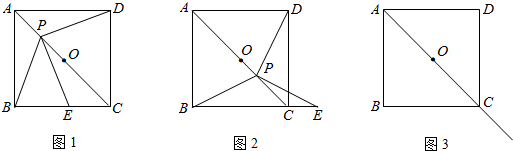
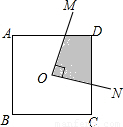
 如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的________.
如图,若O是正方形ABCD的中心,直角∠MON绕O点旋转,则∠MON与正方形围成的四边形的面积是正方形ABCD面积的________.
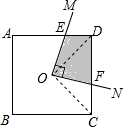 解:连接OD、OC.
解:连接OD、OC.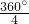 =90°,
=90°,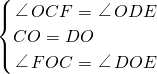
 S,
S, S;
S; .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:《第23章 旋转》2012年单元测试卷(西城区)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com